题目内容
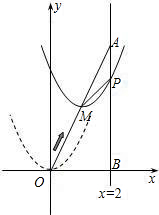 如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P.
如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P.(1)设抛物线顶点M的横坐标为m,
①用m的代数式表示点P的坐标;
②当m为何值时,线段PB最短;
(2)在抛物线平移的过程中,当△PMA是等腰三角形时,求m的值.
考点:二次函数图象与几何变换
专题:
分析:(1)根据A点的坐标,用待定系数法即可求出直线OA的解析式.
①由于M点在直线OA上,可根据直线OA的解析式来表示出M点的坐标,因为M点是平移后抛物线的顶点,因此可用顶点式二次函数通式来设出这个二次函数的解析式,P的横坐标为2,将其代入抛物线的解析式中即可得出P点的坐标.
②PB的长,实际就是P点的纵坐标,因此可根据其纵坐标的表达式来求出PB最短时,对应的m的值.
(2)需要分类讨论:以AP为底和以AP为腰两种情况下的等于三角形,利用两点间的距离公式进行解答即可.
①由于M点在直线OA上,可根据直线OA的解析式来表示出M点的坐标,因为M点是平移后抛物线的顶点,因此可用顶点式二次函数通式来设出这个二次函数的解析式,P的横坐标为2,将其代入抛物线的解析式中即可得出P点的坐标.
②PB的长,实际就是P点的纵坐标,因此可根据其纵坐标的表达式来求出PB最短时,对应的m的值.
(2)需要分类讨论:以AP为底和以AP为腰两种情况下的等于三角形,利用两点间的距离公式进行解答即可.
解答:解:(1)设OA所在直线的函数解析式为y=kx(k≠0),
∵A(2,4),
∴2k=4,
∴k=2,
∴OA所在直线的函数解析式为y=2x.
①∵顶点M的横坐标为m,且在线段OA上移动,
∴y=2m(0≤m≤2).
∴顶点M的坐标为(m,2m).
∴抛物线函数解析式为y=(x-m)2+2m.
∴当x=2时,y=(2-m)2+2m=m2-2m+4(0≤m≤2).
∴点P的坐标是(2,m2-2m+4).
②∵PB=m2-2m+4=(m-1)2+3,
又∵0≤m≤2,
∴当m=1时,PB最短.
(2)由(1)知,M(m,2m)、P(2,m2-2m+4).
当AP=MP时,|m2-2m|=
,
整理,得m2(m-2)2=2(m-2)2.
∵A(2,4),
∴点P、M均不与点A重合,即m≠2,
解得 m=
或m=-
(舍去);
同理,当AP=AM时,m=2,不合题意,舍去;
当AM=MP时,m=
.
综上所述,m的值是
或
.
∵A(2,4),
∴2k=4,
∴k=2,
∴OA所在直线的函数解析式为y=2x.
①∵顶点M的横坐标为m,且在线段OA上移动,
∴y=2m(0≤m≤2).
∴顶点M的坐标为(m,2m).
∴抛物线函数解析式为y=(x-m)2+2m.
∴当x=2时,y=(2-m)2+2m=m2-2m+4(0≤m≤2).

∴点P的坐标是(2,m2-2m+4).
②∵PB=m2-2m+4=(m-1)2+3,
又∵0≤m≤2,
∴当m=1时,PB最短.
(2)由(1)知,M(m,2m)、P(2,m2-2m+4).
当AP=MP时,|m2-2m|=
| (m-2)2+(2m-m2+2m-4)2 |
整理,得m2(m-2)2=2(m-2)2.
∵A(2,4),
∴点P、M均不与点A重合,即m≠2,
解得 m=
| 2 |
| 2 |
同理,当AP=AM时,m=2,不合题意,舍去;
当AM=MP时,m=
| 5 |
综上所述,m的值是
| 2 |
| 5 |
点评:本题考查了一次函数解析式的确定、二次函数图象的平移、函数图象的交点、图形面积的求法等知识点,主要考查学生分类讨论和数形结合的数学思想方法.

练习册系列答案
相关题目
 如图所示,在平行四边形ABCD中,E为边AB的中点,AC、DE相交于点O,已知△OAE的面积为1cm2,那么平行四边形ABCD的面积为
如图所示,在平行四边形ABCD中,E为边AB的中点,AC、DE相交于点O,已知△OAE的面积为1cm2,那么平行四边形ABCD的面积为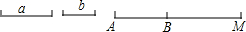 阅读:在用尺规作线段AB等于线段a时,小明的具体作法如下:
阅读:在用尺规作线段AB等于线段a时,小明的具体作法如下: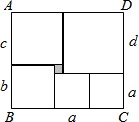 如图,长方形ABCD被分成六个小正方形,已知中间一个小正方形的边长为2,其他正方形的边长分别为a、b、c、d.观察图形并探索:
如图,长方形ABCD被分成六个小正方形,已知中间一个小正方形的边长为2,其他正方形的边长分别为a、b、c、d.观察图形并探索: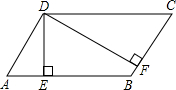 如图,已知在?ABCD中,DE⊥AB于点E,DF⊥BC于点F,若?ABCD的周长为48,DE=5,DF=10,求AB和CD之间的距离及AD和BC之间的距离.
如图,已知在?ABCD中,DE⊥AB于点E,DF⊥BC于点F,若?ABCD的周长为48,DE=5,DF=10,求AB和CD之间的距离及AD和BC之间的距离. 如图,已知?ABCD的周长为10
如图,已知?ABCD的周长为10