题目内容
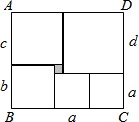 如图,长方形ABCD被分成六个小正方形,已知中间一个小正方形的边长为2,其他正方形的边长分别为a、b、c、d.观察图形并探索:
如图,长方形ABCD被分成六个小正方形,已知中间一个小正方形的边长为2,其他正方形的边长分别为a、b、c、d.观察图形并探索:(1)填空:b=
(2)请求出a的值,并求出长方形ABCD的面积.
考点:整式的加减,列代数式
专题:
分析:(1)利用中间一个小正方形的边长为2,得出b,d与a的关系;
(2)利用c=b+2,b=a+2,得出c=a+4,再利用c=d-2,d=2a-2,得出c=2a-4,那么2a-4=a+4,解方程求出a的值,然后分别计算出长方形ABCD的长与宽,进而求出面积.
(2)利用c=b+2,b=a+2,得出c=a+4,再利用c=d-2,d=2a-2,得出c=2a-4,那么2a-4=a+4,解方程求出a的值,然后分别计算出长方形ABCD的长与宽,进而求出面积.
解答:解:(1)∵中间一个小正方形的边长为2,
∴b=a+2,d=2a-2;
故答案为:a+2,2a-2(或a+6);
(2)∵c=b+2,b=a+2,
∴c=a+4,
又∵c=d-2,d=2a-2,
∴c=2a-4,
∴2a-4=a+4,
解得a=8.
则长方形ABCD的长为c+d=a+4+2a-2=3a+2=26,
宽为a+d=a+2a-2=3a-2=22,
所以长方形ABCD的面积为:26×22=572.
∴b=a+2,d=2a-2;
故答案为:a+2,2a-2(或a+6);
(2)∵c=b+2,b=a+2,
∴c=a+4,
又∵c=d-2,d=2a-2,
∴c=2a-4,
∴2a-4=a+4,
解得a=8.
则长方形ABCD的长为c+d=a+4+2a-2=3a+2=26,
宽为a+d=a+2a-2=3a-2=22,
所以长方形ABCD的面积为:26×22=572.
点评:此题主要考查了一元一次方程的应用,整式的加减,列代数式,利用各边长之间的关系得出等式是解题关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
下列各式正确的是( )
A、
| ||||
B、-
| ||||
| C、0>-19.2 | ||||
| D、3.1<-13 |
一个正方形的边长是m4,则它的面积为( )
| A、m6 |
| B、4m4 |
| C、m12 |
| D、m8 |
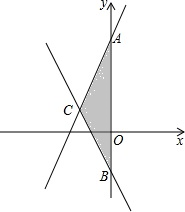 如图,已知直线y=2x+5和y=-x-1相交于点C,且两直线与y轴的交点分别是A,B.
如图,已知直线y=2x+5和y=-x-1相交于点C,且两直线与y轴的交点分别是A,B. 如图,已知∠1=∠2=∠3,据此可以判定哪些直线平行,请说明理由.
如图,已知∠1=∠2=∠3,据此可以判定哪些直线平行,请说明理由.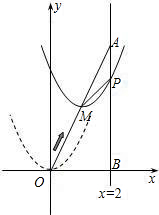 如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P.
如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P.