题目内容
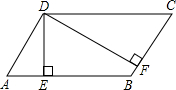 如图,已知在?ABCD中,DE⊥AB于点E,DF⊥BC于点F,若?ABCD的周长为48,DE=5,DF=10,求AB和CD之间的距离及AD和BC之间的距离.
如图,已知在?ABCD中,DE⊥AB于点E,DF⊥BC于点F,若?ABCD的周长为48,DE=5,DF=10,求AB和CD之间的距离及AD和BC之间的距离.考点:平行四边形的性质
专题:
分析:由在?ABCD中,DE⊥AB于点E,DF⊥BC于点F,DE=5,DF=10,根据平行线间的距离定义,即可求得答案.
解答:解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵DE⊥AB,DF⊥BC,DE=5,DF=10,
∴AB和CD之间的距离为:5,AD和BC之间的距离为:10.
∴AB∥CD,AD∥BC,
∵DE⊥AB,DF⊥BC,DE=5,DF=10,
∴AB和CD之间的距离为:5,AD和BC之间的距离为:10.
点评:此题考查了平行四边形的性质.此题比较简单,注意掌握数形结合思想的应用.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
下列各式正确的是( )
A、
| ||||
B、-
| ||||
| C、0>-19.2 | ||||
| D、3.1<-13 |
下列运算正确的是( )
| A、x7÷x5=x2 | ||
| B、2a+3b=5ab | ||
C、
| ||
| D、992=(100-1)2=1002-1 |
一个正方形的边长是m4,则它的面积为( )
| A、m6 |
| B、4m4 |
| C、m12 |
| D、m8 |
已知函数y=
,则下列说法正确的是( )
| 6 |
| x |
| A、点(-2,-3)一定在此函数的图象上 |
| B、此函数的图象只在第一象限 |
| C、y随x增大而增大 |
| D、当x<0时,y>0 |
 已知:如图,在?ABCD中,从顶点D向AB作垂线,垂足为E,且E是AB的中点,已知?ABCD的周长为8.6cm,△ABD的周长为6cm.求AB、BC的长.
已知:如图,在?ABCD中,从顶点D向AB作垂线,垂足为E,且E是AB的中点,已知?ABCD的周长为8.6cm,△ABD的周长为6cm.求AB、BC的长.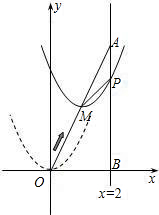 如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P.
如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P. 如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积.
如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积.