题目内容
14.某种产品的成本是120元/件,试销阶段每件产品的售价x(元)与产品的日销量y(件)之间关系如表所示:| x/元 | 130 | 150 | 165 |
| y/件 | 70 | 50 | 35 |
分析 根据题意可以得到y与x的关系式,从而可以得到利润与x的函数关系,从而可以解答本题.
解答 解:设y与x之间的函数关系为y=kx+b,
$\left\{\begin{array}{l}{130k+b=70}\\{150k+b=50}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=200}\end{array}\right.$,
∴y与x之间的函数关系为y=-x+200,
设获得的利润为w元,
w=(x-120)(-x+200)=-(x-160)2+1600,
∴当x=160时,w取得最大值,此时w=1600,
即要使每天所获得最大的利润,每件产品的销售价应定为160元,此时每天的销售利润是1600元.
点评 本题考查二次函数的应用,解题的关键是明确题意,列出相应的函数关系式,会求二次函数的最值.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
3.某车间有26名工人,每人每天可以生产800个螺栓或1 000个螺母,1个螺栓需要配2个螺母,为使每天生产的螺栓和螺母刚好配套,设安排x名工人生产螺栓,则下面所列方程正确的是( )
| A. | 2×1 000(26-x)=800x | B. | 1 000(13-x)=800x | ||
| C. | 1 000(26-x)=2×800x | D. | 1 000(26-x)=800x |
 如图,l1∥l2∥l3,AM=3,MB=5,CM=4.5,EF=16,求DM,EK,KF的值.
如图,l1∥l2∥l3,AM=3,MB=5,CM=4.5,EF=16,求DM,EK,KF的值.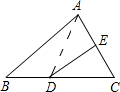 如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,求△ABD的周长.
如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,求△ABD的周长. 如图,△ABC中,AB=AC,2条中线BD、CE相交于点O,图中有全等的三角形吗?如有,请写出来,并选其中一对证明.
如图,△ABC中,AB=AC,2条中线BD、CE相交于点O,图中有全等的三角形吗?如有,请写出来,并选其中一对证明.