题目内容

13．在一个直角三角形中，已知它的周长是40cm，斜边上的中线为8.5cm，则这个直角三角形的面积60cm2．

分析 利用直角三角形的性质得出斜边长，再利用勾股定理得出直角边长，即可得出三角形面积．

解答 解：∵一个直角三角形，斜边上的中线为8.5cm，
∴斜边长为：17cm，
∵它的周长是40cm，
∴两条直角边长为：23cm，
设一条直角边长为：xcm，则另一条边长为：（23-x）cm，
故x2+（23-x）2=172，
解得：x1=8，x2=15，
故这个直角三角形的面积为：$\frac{1}{2}$×8×15=60（cm2）．
故答案为：60cm2．

点评 此题主要考查了勾股定理以及直角三角形的性质，得出直角边长是解题关键．

练习册系列答案
相关题目
3．阅读下列材料并解决有关问题：
我们知道|x|=$\left\{\begin{array}{l}{x（x＞0）}\\{0（x=0）}\\{-x（x＜0）}\end{array}\right.$现在我们可以用这一结论来化简含有绝对值的代数式，如化简代数式|x+1|+|x-2|时，可令x+1=0和x-2=0，分别求得x=-1和x=2（称-1，2分别为|x+1|与|x-2|的零点值）．在有理数范围内，零点值x=-1和x=2可将全体有理数分成不重复且不遗漏的如下3种情况：（1）x＜-1；（2）-1≤x＜2；（3）x≥2．从而化简代数式|x+1|+|x-2|可分以下3种情况：
（1）当x＜-1时，原式=-（x+1）-（x-2）=-2x+1；
（2）当-1≤x＜2时，原式=x+1-（x-2）=3；
（3）当x≥2时，原式=x+1+x-2=2x-1．
综上讨论，原式=$\left\{\begin{array}{l}{-2x+1（x＜-1）}\\{2（-1≤x＜2）}\\{2x-1（x≥2）}\end{array}\right.$
通过以上阅读，请你解决以下问题：
（1）分别求出|x+2|和|x-4|的零点值；
（2）化简代数式|x+2|+|x-4|；
（3）解方程|x+2|+|x-4|=8．
4．已知α是锐角，cosα=$\frac{1}{3}$，则tanα的值是（　　）
A．$\frac{\sqrt{3}}{10}$B．2$\sqrt{2}$C．3D．$\sqrt{10}$
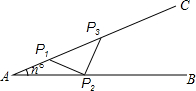1．如图钢架中，∠A=n°，依次焊上等长的钢条P1P2，P2P3，…，来加固钢架，若P1A=P1P2，要使得这样的钢条只能焊上4根，则n的取值范围是18≤n＜22.5．
8．（1）先化简，再求值：$\frac{1}{4}$x2+2（x-$\frac{2}{3}$y2）-$\frac{1}{3}$（-3x2+2y2）-$\frac{1}{2}$x，其中x=2，y=-3．
（2）已知A=2a2-a，B=-5a+1．
①化简：3A-2B+2；
②当a=-$\frac{1}{2}$时，求3A-2B+2的值．
18．已知$\frac{a}{b}=\frac{c}{d}=\frac{2}{3}$（b+d≠0），求$\frac{a+c}{b+d}$的值．
5．（1）画一条线段AB=3cm；
（2）分别以A、B为圆心，以2cm为半径画圆，⊙A，⊙B相交于M，N两点．
2．如图，点C是AB的黄金分割点，
（1）若AB=1，则AC=$\frac{\sqrt{5}-1}{2}$≈0.618，BC=$\frac{3-\sqrt{5}}{2}$≈0.382；
（2）若AC=1，求BC、AB；
（3）若BC=1，求AC、AB．
3．如图是由几个小立方体所搭几何体的俯视图，小正方形中的数字表示在该位置的小立方体的层数，请画出这个几何体的主视图和左视图．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网