题目内容
16.已知关于x的函数y=ax2+x+1-a(a为常数)(1)若函数的图象与坐标轴恰有两个交点,求a的值;
(2)若函数的图象是抛物线,开口向上且顶点在x轴下方,求a的取值范围.
分析 (1)a=0时,函数为一次函数;当a≠0时,△=0或1-a=0时函数的图象与坐标轴恰有两个交点;
(2)开口向上可知a>0,顶点在x轴下方则△>0.
解答 解:(1)当a=0时,y=x+1与x轴和y轴各有一个交点,
当a≠0时该函数是二次函数,分两种情况:
①△=0,即12-4a(1-a)=0,解得a=$\frac{1}{2}$
②1-a=0,解得,a=1
所以a的取值是0、$\frac{1}{2}$、1.
(2)∵开口向上,顶点在x轴的下方,
∴a>0,且△=12-4a(1-a)=1-4a+4a2=(1-2a)2>0.
∴a>0,且a≠$\frac{1}{2}$.
点评 本题主要考查的是抛物线与x轴的交点,熟练掌握二次函数的图象和性质是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
4.已知α是锐角,cosα=$\frac{1}{3}$,则tanα的值是( )
| A. | $\frac{\sqrt{3}}{10}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
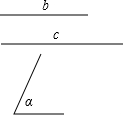 已知两线段b,c(b<c)及∠α,求作△ABC,使得AB=c,∠BAC=∠α,∠BAC的平分线AD=b.(只保留作图痕迹,不要求写出作法)
已知两线段b,c(b<c)及∠α,求作△ABC,使得AB=c,∠BAC=∠α,∠BAC的平分线AD=b.(只保留作图痕迹,不要求写出作法)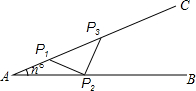 如图钢架中,∠A=n°,依次焊上等长的钢条P1P2,P2P3,…,来加固钢架,若P1A=P1P2,要使得这样的钢条只能焊上4根,则n的取值范围是18≤n<22.5.
如图钢架中,∠A=n°,依次焊上等长的钢条P1P2,P2P3,…,来加固钢架,若P1A=P1P2,要使得这样的钢条只能焊上4根,则n的取值范围是18≤n<22.5.