题目内容
19．解不等式：$\frac{x}{6}$-1＞$\frac{x-2}{3}$，并把它的解集在数轴上表示出来．
分析 首先去分母，然后去括号，移项合并，系数化为1，即可求得答案．注意系数化1时，因为系数是-1，所以不等号的方向要发生改变，在数轴上表示时：注意此题为空心点，方向向左．
解答 解：去分母，得x-6＞2（x-2）．
去括号，得x-6＞2x-4，
移项，得x-2x＞-4+6，
合并同类项，得-x＞2，
系数化为1，得x＜-2，
这个不等式的解集在数轴上表示如下图所示．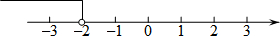
点评 此题考查了一元一次不等式的解法．注意解不等式依据不等式的基本性质，特别是在系数化为1这一个过程中要注意不等号的方向的变化．去分母的过程中注意不能漏乘没有分母的项．用数轴表示不等式的解集时：注意时实心点还是空心点，方向是向右还是向左．
练习册系列答案
名校课堂系列答案
相关题目
7．
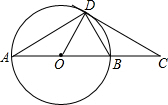如图，AB是⊙O的直径，CD是⊙O的切线，切点为D，DC与AB的延长线交于点C，∠A=30°，给出下面3个结论：∠BDC=∠A；AB=2BC；AD2=3BC2；其中正确结论的个数是（ ）
如图，AB是⊙O的直径，CD是⊙O的切线，切点为D，DC与AB的延长线交于点C，∠A=30°，给出下面3个结论：∠BDC=∠A；AB=2BC；AD2=3BC2；其中正确结论的个数是（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
11．方程组$\left\{\begin{array}{l}{x+3y=5}\\{2x-3y=1}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$ |