题目内容
20.为了了解某校七年级学生的课外阅读量,随机调查了该校15名七年级学生,统计如下:| 阅读量(单位:本/周) | 0 | 1 | 2 | 3 | 4 |
| 人数(单位:人) | 1 | 4 | 6 | 2 | 2 |
| A. | 中位数是2 | B. | 平均数是2 | C. | 众数是2 | D. | 方差是2 |
分析 根据方差、中位数、众数和平均数的计算公式分别进行计算,即可得出答案.
解答 解:A、把这些数字从小到大排列,最中间的数是2,则中位数是2,故本选项正确;
B、平均数是:$\frac{1}{15}$(1×4+2×6+3×2+4×2)=2,故本选项正确;
C、2出现了6次,出现的次数最多,则众数是2,故本选项正确;
D、方差是:$\frac{1}{15}$[(0-2)2+4(1-2)2+6(2-2)2+2(3-2)2+2(4-2)2]=1.2,故本选项错误;
故选D.
点评 本题考查了方差、中位数、众数和平均数的知识,掌握各知识点的计算公式和概念是解题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
10.已知x为正整数,y、z与x的关系如表格所示,根据表格中的数字变化规律,解答下列问题.
(1)分别写出y与x,z与x之间的关系式;
(2)是否存在x的值,使得y与z相等?若存在,求出这个值;若不存在,请说明理由.
| x | y | z |
| … | … | … |
| 3 | 10×3+60 | 2×10 |
| 4 | 10×4+60 | 2×11 |
| 5 | 10×5+60 | 2×12 |
| … | … | … |
(2)是否存在x的值,使得y与z相等?若存在,求出这个值;若不存在,请说明理由.
8.关于反比例函数y=$\frac{3}{x}$,下列说法中正确的是( )
| A. | 它的图象分布在第二、四象限 | B. | 它的图象过点(-6,-2) | ||
| C. | 当x<0时,y的值随x的增大而减小 | D. | 与y轴的交点是(0,3) |
12.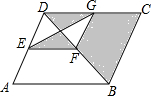 小强喜欢玩飞镖游戏,一天他用平行四边形做了一个飞镖盘,如图所示,?ABCD中,过对角线BD上任一点F分别作FE∥AB,FG∥BC分别交AD,CD于点E,G,连接EG,则小强随机掷一次飞镖,飞镖落在阴影部分的概率是( )
小强喜欢玩飞镖游戏,一天他用平行四边形做了一个飞镖盘,如图所示,?ABCD中,过对角线BD上任一点F分别作FE∥AB,FG∥BC分别交AD,CD于点E,G,连接EG,则小强随机掷一次飞镖,飞镖落在阴影部分的概率是( )
 小强喜欢玩飞镖游戏,一天他用平行四边形做了一个飞镖盘,如图所示,?ABCD中,过对角线BD上任一点F分别作FE∥AB,FG∥BC分别交AD,CD于点E,G,连接EG,则小强随机掷一次飞镖,飞镖落在阴影部分的概率是( )
小强喜欢玩飞镖游戏,一天他用平行四边形做了一个飞镖盘,如图所示,?ABCD中,过对角线BD上任一点F分别作FE∥AB,FG∥BC分别交AD,CD于点E,G,连接EG,则小强随机掷一次飞镖,飞镖落在阴影部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{5}$ |
9.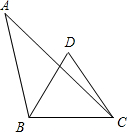 如图,点D为线段AB与线段BC的垂直平分线的交点,连接AC、BD、DC,若∠A=35°,∠ABD=44°,则∠DCA的度数为( )
如图,点D为线段AB与线段BC的垂直平分线的交点,连接AC、BD、DC,若∠A=35°,∠ABD=44°,则∠DCA的度数为( )
 如图,点D为线段AB与线段BC的垂直平分线的交点,连接AC、BD、DC,若∠A=35°,∠ABD=44°,则∠DCA的度数为( )
如图,点D为线段AB与线段BC的垂直平分线的交点,连接AC、BD、DC,若∠A=35°,∠ABD=44°,则∠DCA的度数为( )| A. | 10° | B. | 18° | C. | 15° | D. | 9° |
10.函数y=$\frac{1}{x+1}$中自变量x的取值范围是( )
| A. | x≥-1 | B. | x≤-1 | C. | x≠-1 | D. | x=-1 |
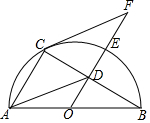 如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.
如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.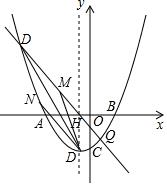 抛物线y=$\frac{1}{3}$x2+bx+c经过点A(-4,0)、B(2,0)两点,与y轴交于点C,顶点为D,对称轴与x轴交于点H,过点H的直线m交抛物线于P、Q两点,其中点P位于第二象限,点Q在y轴的右侧.
抛物线y=$\frac{1}{3}$x2+bx+c经过点A(-4,0)、B(2,0)两点,与y轴交于点C,顶点为D,对称轴与x轴交于点H,过点H的直线m交抛物线于P、Q两点,其中点P位于第二象限,点Q在y轴的右侧.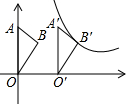 如图,在平面直角坐标系xOy中,点A在y轴上,点B的坐标为(1,2),将△AOB沿x轴向右平移得到△A′O′B′,点B的对应点B′恰好在函数y=$\frac{6}{x}$(x>0)的图象上,此时点A移动的距离为2.
如图,在平面直角坐标系xOy中,点A在y轴上,点B的坐标为(1,2),将△AOB沿x轴向右平移得到△A′O′B′,点B的对应点B′恰好在函数y=$\frac{6}{x}$(x>0)的图象上,此时点A移动的距离为2.