题目内容
11.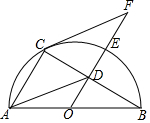 如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.
如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.(1)求证:CF为⊙O的切线;
(2)若DE=1,∠ABC=30°.①求⊙O的半径;②求sin∠BAD的值.
(3)若四边形ACFD是平行四边形,求sin∠BAD的值.
分析 (1)欲证明CF为⊙O的切线,只要证明即OC⊥CF即可;
(2)①设⊙O的半径为r.由OD⊥BC 且∠ABC=30°,可得OD=$\frac{1}{2}$OB=$\frac{1}{2}$r,又DE=1,且OE=OD+DE,列出方程即可解决问题;
②作DH⊥AB于H,求出DH、AD即可解决问题;
(3)设⊙O的半径为r.想办法用r表示DH、AD即可解决问题;
解答 解:(1)连接CO.
∵D为BC的中点,且OB=OC,
∴OD⊥BC,
∵OB=OC,
∴∠OBC=∠OCB,
又∵∠OBC=∠OFC,
∴∠OCB=∠OFC,
∵OD⊥BC,
∴∠DCF+∠OFC=90°.
∴∠DCF+∠OCB=90°.即OC⊥CF,
∴CF为⊙O的切线.
(2)①设⊙O的半径为r.
∵OD⊥BC 且∠ABC=30°,
∴OD=$\frac{1}{2}$OB=$\frac{1}{2}$r,
又∵DE=1,且OE=OD+DE,
∴$r=1+\frac{1}{2}r$,解得:r=2,
②作DH⊥AB于H,在Rt△ODH中,∠DOH=60°,OD=1.
∴DH=$\frac{{\sqrt{3}}}{2}$,OH=$\frac{1}{2}$,
在Rt△DAH中,∵AH=AO+OH=$\frac{5}{2}$,
∴由勾股定理:AD=$\sqrt{7}$.
∴$sin∠BAD=\frac{DH}{AD}=\frac{{\sqrt{3}}}{{2\sqrt{7}}}=\frac{{\sqrt{21}}}{14}$.
(3)设⊙O的半径为r.
∵O、D分别为AB、BC中点,
∴AC=2OD,
又∵四边形ACFD是平行四边形,
∴DF=AC=2OD,
∵∠OBC=∠OFC,∠CDF=∠ODB=90°,
∴△ODB∽△CDF,
∴$\frac{OD}{CD}=\frac{BD}{DF}$,
∴$\frac{OD}{BD}=\frac{BD}{2OD}$,解得:$BD=\sqrt{2}OD$,
∴在Rt△OBD中,OB=r,
∴$OD=\frac{{\sqrt{3}}}{3}r,BD=\frac{{\sqrt{6}}}{3}r$,
∴$OH=\frac{1}{3}r,DH=\frac{{\sqrt{2}}}{3}r$,
∴在Rt△DAH中,∵AH=AO+OH=$\frac{4}{3}r$,
∴由勾股定理:AD=$\sqrt{2}r$,
∴$sin∠BAD=\frac{DH}{AD}=\frac{{\sqrt{2}r}}{{3\sqrt{2}r}}=\frac{1}{3}$.
点评 本题考查切线的判定和性质、解直角三角形、平行四边形的性质、锐角三角函数、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造直角三角形解决问题.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案| A. | 3>|-7| | B. | $\sqrt{12}$>3$\sqrt{2}$ | C. | 0<-2 | D. | ($\frac{1}{2}$)2<3-1 |
| A. | (2,3) | B. | (-3,2) | C. | (-2,3) | D. | (3,-2) |
| 阅读量(单位:本/周) | 0 | 1 | 2 | 3 | 4 |
| 人数(单位:人) | 1 | 4 | 6 | 2 | 2 |
| A. | 中位数是2 | B. | 平均数是2 | C. | 众数是2 | D. | 方差是2 |
| A. |  | B. |  | C. |  | D. |  |
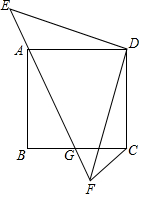 如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.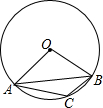 如图,△ABC为⊙O的内接三角形,∠AOB=100°,则∠ACB的度数为130°.
如图,△ABC为⊙O的内接三角形,∠AOB=100°,则∠ACB的度数为130°.