题目内容
12.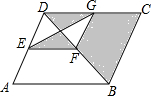 小强喜欢玩飞镖游戏,一天他用平行四边形做了一个飞镖盘,如图所示,?ABCD中,过对角线BD上任一点F分别作FE∥AB,FG∥BC分别交AD,CD于点E,G,连接EG,则小强随机掷一次飞镖,飞镖落在阴影部分的概率是( )
小强喜欢玩飞镖游戏,一天他用平行四边形做了一个飞镖盘,如图所示,?ABCD中,过对角线BD上任一点F分别作FE∥AB,FG∥BC分别交AD,CD于点E,G,连接EG,则小强随机掷一次飞镖,飞镖落在阴影部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{5}$ |
分析 根据题意可以求得阴影部分的面积占整个平行四边形ABCD的比重,从而可以求得飞镖落在阴影部分的概率.
解答  解:如右图所示,EG与DF交于点O,
解:如右图所示,EG与DF交于点O,
由题意可得,
四边形EFGD是平行四边形,
则OE=OG,
∴△OEF的面积等于△OCF的面积,
∴阴影部分的面积是?ABCD面积的一半,
∴飞镖落在阴影部分的概率是$\frac{1}{2}$,
故选B.
点评 本题考查几何概率,解答本题的关键是明确题意,求出阴影部分的面积占整个平行四边形ABCD的比重.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
3.在平面直角坐标系中有点P(3,2),点P和点P′关于直线y=x对称,那么点P′的坐标为( )
| A. | (2,3) | B. | (-3,2) | C. | (-2,3) | D. | (3,-2) |
20.为了了解某校七年级学生的课外阅读量,随机调查了该校15名七年级学生,统计如下:
则下列说法错误的是( )
| 阅读量(单位:本/周) | 0 | 1 | 2 | 3 | 4 |
| 人数(单位:人) | 1 | 4 | 6 | 2 | 2 |
| A. | 中位数是2 | B. | 平均数是2 | C. | 众数是2 | D. | 方差是2 |
4.若2x+5y-3=0,则4x•32y的值为( )
| A. | 8 | B. | -8 | C. | $\frac{1}{8}$ | D. | -$\frac{1}{8}$ |
1.下列银行标志图中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.计算3$\sqrt{2}$-4$\sqrt{2}$的结果是( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 7$\sqrt{2}$ | D. | -1 |
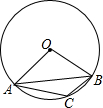 如图,△ABC为⊙O的内接三角形,∠AOB=100°,则∠ACB的度数为130°.
如图,△ABC为⊙O的内接三角形,∠AOB=100°,则∠ACB的度数为130°. 如图,以△ABC的边BC为直径的圆O分别交AB,AC于点D,E,连接OD、OE.若
如图,以△ABC的边BC为直径的圆O分别交AB,AC于点D,E,连接OD、OE.若 如图,在?ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S?AEPH=4.
如图,在?ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S?AEPH=4.