题目内容
 如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(10,0)、(10,3)、(4,3).点P从原点、点Q 从B点同时出发,分别作匀速运动,点P沿OA以每秒1个单位向终点A运动,点Q沿BC、以每秒2个单位向终点C运动.当这两点中有一点到达自己的终点时,另一点也停止运动.
如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(10,0)、(10,3)、(4,3).点P从原点、点Q 从B点同时出发,分别作匀速运动,点P沿OA以每秒1个单位向终点A运动,点Q沿BC、以每秒2个单位向终点C运动.当这两点中有一点到达自己的终点时,另一点也停止运动.(1)设从出发起运动了x秒,求Q点的坐标;
(2)当x等于多少时,四边形OPQC为平行四边形?
(3)四边形OPQC能否成为等腰梯形?若成,求出x的值,若不成说明理由.
考点:相似形综合题
专题:
分析:(1)因为Q沿BC运动,BC∥OA,所以点Q的纵坐标为3,以每秒2个单位运动,所以从出发起运动了x秒,运动了2x,故Q点的坐标横坐标为10-2x,即可得Q点的坐标;
(2)由A、B、C的坐标分别为(10,0)、(10,3)、(4,3).可得OC=
=5,BC=10-4=6,OA=10,又由当点Q在BC上,且OP=CQ时,四边形OPQC为平行四边形,即可得方程:x=6-2x,解此方程即可求得答案;
(3)首先过点C作CE⊥OA于点E,过点Q作QF⊥OP于点F,由当OP=CQ+OE+PF时,四边形OPQC成为等腰梯形,即可得方程:x=4+(6-2x)+4,解此方程即可求得答案.
(2)由A、B、C的坐标分别为(10,0)、(10,3)、(4,3).可得OC=
| 42-32 |
(3)首先过点C作CE⊥OA于点E,过点Q作QF⊥OP于点F,由当OP=CQ+OE+PF时,四边形OPQC成为等腰梯形,即可得方程:x=4+(6-2x)+4,解此方程即可求得答案.
解答:解:(1)∵BC∥OA,
∴点Q的纵坐标为3,
∵以每秒2个单位运动,所以从出发起运动了x秒,运动了2x,
∴Q点的坐标横坐标为10-2x,
∴Q点的坐标为(10-2x,3);
(2)∵A、B、C的坐标分别为(10,0)、(10,3)、(4,3).
∴OC=
=5,BC=10-4=6,OA=10,
∵BC∥OA,
∴当点Q在BC上,且OP=CQ时,四边形OPQC为平行四边形,
∴x=6-2x,
解得x=2;
∴当x等于2时,四边形OPQC为平行四边形;
(3)不能,
理由:过点C作CE⊥OA于点E,过点Q作QF⊥OP于点F,

∵AO∥BC,
∴CE=QF,
当OE=PF=4时,△OCE≌△PQF(SAS),
此时四边形OPQC成为等腰梯形,
即OP=OE+CQ+PF,
∴x=4+(6-2x)+4,
解得x=
,
∵
×2=
>6,
∴四边形OPQC不能成为等腰梯形.
∴点Q的纵坐标为3,
∵以每秒2个单位运动,所以从出发起运动了x秒,运动了2x,
∴Q点的坐标横坐标为10-2x,
∴Q点的坐标为(10-2x,3);
(2)∵A、B、C的坐标分别为(10,0)、(10,3)、(4,3).
∴OC=
| 32+42 |
∵BC∥OA,
∴当点Q在BC上,且OP=CQ时,四边形OPQC为平行四边形,
∴x=6-2x,
解得x=2;
∴当x等于2时,四边形OPQC为平行四边形;
(3)不能,
理由:过点C作CE⊥OA于点E,过点Q作QF⊥OP于点F,

∵AO∥BC,
∴CE=QF,
当OE=PF=4时,△OCE≌△PQF(SAS),
此时四边形OPQC成为等腰梯形,
即OP=OE+CQ+PF,
∴x=4+(6-2x)+4,
解得x=
| 14 |
| 3 |
∵
| 14 |
| 3 |
| 28 |
| 3 |
∴四边形OPQC不能成为等腰梯形.
点评:此题考查了梯形的性质、平行四边形的判定与性质以及等腰梯形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在⊙O中,AB是⊙O的弦,过点O作OC⊥AB于点C,连结OB.若AB=4,OC=1,则⊙O的半径为
如图,在⊙O中,AB是⊙O的弦,过点O作OC⊥AB于点C,连结OB.若AB=4,OC=1,则⊙O的半径为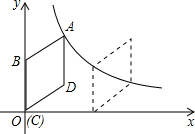 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的
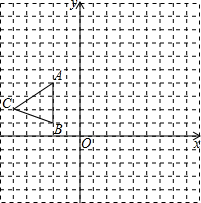 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2). 如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°.
如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长l为
如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长l为