题目内容
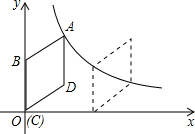 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=
| k |
| x |
(1)求k的值.
(2)若将菱形ABCD向右平移,使点D落在反比例函数y=
| k |
| x |
(3)怎样平移可以使点B、D同时落在第一象限的曲线上?
考点:反比例函数综合题
专题:
分析:(1)根据点D的坐标为(4,3),即可得出DE的长以及DO的长,即可得出A点坐标,进而求出k的值;
(2)根据D′F′的长度即可得出D′点的纵坐标,进而利用反比例函数的性质求出OF′的长,即可得出答案;
(3)根据平移的特点,可得B、D平移后得坐标,根据图象在第一象限的曲线上,可得向右平移的单位,向下平移的单位,可得答案.
(2)根据D′F′的长度即可得出D′点的纵坐标,进而利用反比例函数的性质求出OF′的长,即可得出答案;
(3)根据平移的特点,可得B、D平移后得坐标,根据图象在第一象限的曲线上,可得向右平移的单位,向下平移的单位,可得答案.
解答:解:(1)作DE⊥BO,DF⊥x轴于点F, ,
,
∵点D的坐标为(4,3),
∴FO=4,DF=3,
∴DO=5,
∴AD=5,
∴A点坐标为:(4,8),
∴xy=4×8=32,
∴k=32;
(2)∵将菱形ABCD向右平移,使点D落在反比例函数y=
(x>0)的图象上,
∴DF=3,D′F′=3,
∴D′点的纵坐标为3,
∴3=
,
x=
,
∴OF′=
,
∴FF′=
-4=
,
∴菱形ABCD向右平移的距离为:
;
(3)图象向右平移m个单位,向下平移n个单位,
B(0+m,5-n),D(4+m,3-n)在y=
图象上,
,
解得
.
则菱形向右平移2
-2个单位,下移
个单位,点B、D同时落在第一象限的曲线上.
 ,
,∵点D的坐标为(4,3),
∴FO=4,DF=3,
∴DO=5,
∴AD=5,
∴A点坐标为:(4,8),
∴xy=4×8=32,
∴k=32;
(2)∵将菱形ABCD向右平移,使点D落在反比例函数y=
| 32 |
| x |
∴DF=3,D′F′=3,
∴D′点的纵坐标为3,
∴3=
| 32 |
| x |
x=
| 32 |
| 3 |
∴OF′=
| 32 |
| 3 |
∴FF′=
| 32 |
| 3 |
| 20 |
| 3 |
∴菱形ABCD向右平移的距离为:
| 20 |
| 3 |
(3)图象向右平移m个单位,向下平移n个单位,
B(0+m,5-n),D(4+m,3-n)在y=
| 32 |
| x |
|
解得
|
则菱形向右平移2
| 13 |
11-4
| ||
| 3 |
点评:本题主要考查了反比例函数的综合题,利用了菱形的性质,利用了平移的特点,根据已知得出A点坐标是解题关键.

练习册系列答案
相关题目
数据:2,5,4,5,3,4,4的众数与中位数分别是( )
| A、4,3 | B、4,4 |
| C、3,4 | D、4,5 |
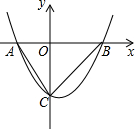 如图所示,二次函数y=x2-x-6的图象交x轴于A、B两点,交y轴于C点.
如图所示,二次函数y=x2-x-6的图象交x轴于A、B两点,交y轴于C点. 如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路. 如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程.
如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程. 如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(10,0)、(10,3)、(4,3).点P从原点、点Q 从B点同时出发,分别作匀速运动,点P沿OA以每秒1个单位向终点A运动,点Q沿BC、以每秒2个单位向终点C运动.当这两点中有一点到达自己的终点时,另一点也停止运动.
如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(10,0)、(10,3)、(4,3).点P从原点、点Q 从B点同时出发,分别作匀速运动,点P沿OA以每秒1个单位向终点A运动,点Q沿BC、以每秒2个单位向终点C运动.当这两点中有一点到达自己的终点时,另一点也停止运动.