题目内容
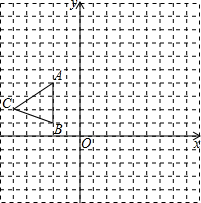 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).(1)请画出△ABC关于x轴对称的△A1B1C1.
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2,B2,C2,请画出△A2B2C2.
(3)求△A1B1C1与△A2B2C2的面积比,即S△A1B1C1:S△A2B2C2=
考点:作图-位似变换,作图-轴对称变换
专题:作图题
分析:(1)根据关于x轴对称点的性质得出对应点位置进而得出答案;
(2)根据将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得出各点坐标,进而得出答案;
(3)利用位似图形的性质得出位似比,进而得出答案.
(2)根据将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得出各点坐标,进而得出答案;
(3)利用位似图形的性质得出位似比,进而得出答案.
解答: 解:(1)如图所示:△A1B1C1即为所求;
解:(1)如图所示:△A1B1C1即为所求;
(2)如图所示:△A2B2C2即为所求;
(3)∵将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2,B2,C2,
∴△A1B1C1与△A2B2C2的相似比为:1:2,
∴S△A1B1C1:S△A2B2C2=1:4.
故答案为:1:4.
 解:(1)如图所示:△A1B1C1即为所求;
解:(1)如图所示:△A1B1C1即为所求;(2)如图所示:△A2B2C2即为所求;
(3)∵将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2,B2,C2,
∴△A1B1C1与△A2B2C2的相似比为:1:2,
∴S△A1B1C1:S△A2B2C2=1:4.
故答案为:1:4.
点评:此题主要考查了位似变换以及轴对称变换,得出对应点位置是解题关键.

练习册系列答案
相关题目
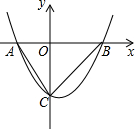 如图所示,二次函数y=x2-x-6的图象交x轴于A、B两点,交y轴于C点.
如图所示,二次函数y=x2-x-6的图象交x轴于A、B两点,交y轴于C点. 如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程.
如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程. 如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(10,0)、(10,3)、(4,3).点P从原点、点Q 从B点同时出发,分别作匀速运动,点P沿OA以每秒1个单位向终点A运动,点Q沿BC、以每秒2个单位向终点C运动.当这两点中有一点到达自己的终点时,另一点也停止运动.
如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(10,0)、(10,3)、(4,3).点P从原点、点Q 从B点同时出发,分别作匀速运动,点P沿OA以每秒1个单位向终点A运动,点Q沿BC、以每秒2个单位向终点C运动.当这两点中有一点到达自己的终点时,另一点也停止运动. 如图:AB∥DC,∠A=∠C,试说明AD∥BC,并每一步注明理由.
如图:AB∥DC,∠A=∠C,试说明AD∥BC,并每一步注明理由.