题目内容
2.已知二次函数的图象与y=-$\frac{1}{3}$x2的图象形状大小,开口方向相同,且顶点坐标是(1,3),那么这个二次函数的解析式是y=-$\frac{1}{3}$(x-1)2+3.分析 设抛物线的解析式为y=a(x+h)2+k,由条件可以得出a=-$\frac{1}{3}$,再将顶点坐标代入解析式就可以求出结论.
解答 解:设抛物线的解析式为y=a(x+h)2+k,且该抛物线的形状与开口方向和抛物线y=-$\frac{1}{3}$x2的相同,
∴a=-$\frac{1}{3}$,
∴y=-$\frac{1}{3}$(x+h)2+k,
∵顶点坐标是(1,3),
∴y=-$\frac{1}{3}$(x-1)2+3,
∴这个函数解析式为y=-$\frac{1}{3}$(x-1)2+3.
故答案为:y=-$\frac{1}{3}$(x-1)2+3.
点评 本题考查了根据顶点坐标运用待定系数法求二次函数的解析式的运用,在解答时运用抛物线的性质求出a值是关健.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知反比例函数y=$\frac{k}{x}$图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,-1),
已知反比例函数y=$\frac{k}{x}$图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,-1), 如图,△ABC中,DF平分∠BDE,EF平分∠DEC,求证:AF平分∠BAC.
如图,△ABC中,DF平分∠BDE,EF平分∠DEC,求证:AF平分∠BAC. 如图,在△ABC中,∠A=90°,BD是角平分线,若AB=8,BC=10,S△ABD=$\frac{32}{3}$,求△BDC的面积.
如图,在△ABC中,∠A=90°,BD是角平分线,若AB=8,BC=10,S△ABD=$\frac{32}{3}$,求△BDC的面积.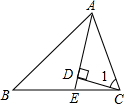 如图,AD平分∠BAC,CD⊥AD,垂足为D,求证:∠1>∠B.
如图,AD平分∠BAC,CD⊥AD,垂足为D,求证:∠1>∠B.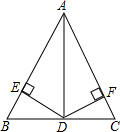 如图,在△ABC中,AD平分∠BAC交BC于D,DE⊥AB于E,DF⊥AC于F,EB=FC.求证:BD=CD.
如图,在△ABC中,AD平分∠BAC交BC于D,DE⊥AB于E,DF⊥AC于F,EB=FC.求证:BD=CD.