��Ŀ����
���κ���y=ax2+bx+c��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ���±���
X | ��1 | 0 | 1 | 3 |
y | ��1 | 3 | 5 | 3 |
���н��ۣ�
��ac��0��
�Ƶ�x��1ʱ��y��ֵ��xֵ���������С��
��3�Ƿ���ax2+��b��1��x+c=0��һ������
�ȵ���1��x��3ʱ��ax2+��b��1��x+c��0��
������ȷ�ĸ���Ϊ�� ��
A. 4�� B. 3�� C. 2�� D. 1��
 B
�����������������-1��-1������0,3������1,5����
��
���,y=-.�Գ���,,
(1)��ȷ����2���������£��Գ��ᣬx��1ʱy�������ټ�С,����3��+2,��ã� .��ȷ����4��+2,�����ɣ�3���õ�������x��Ľ��㣬��ͼ֪����1��x��3ʱ,y>0��ȷ.
���ԣ�1����3����4����ȷ.ѡB.
B
�����������������-1��-1������0,3������1,5����
��
���,y=-.�Գ���,,
(1)��ȷ����2���������£��Գ��ᣬx��1ʱy�������ټ�С,����3��+2,��ã� .��ȷ����4��+2,�����ɣ�3���õ�������x��Ľ��㣬��ͼ֪����1��x��3ʱ,y>0��ȷ.
���ԣ�1����3����4����ȷ.ѡB.
��ͼ����?ABCD�У�P��CD����һ�㣬��AP��BP�ֱ�ƽ�֡�DAB�͡�CBA����AD=5��AP=8�����APB���ܳ���_______��
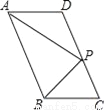
 24
��������������������ı���ABCD��ƽ���ı��Σ�
��AD��CB��AB��CD��
���DAB����CBA��180�㣬
�֡�AP��BP�ֱ�ƽ�֡�DAB�͡�CBA��
���PAB����PBA�� (��DAB����CBA)��90�㣬
�ڡ�APB�У���APB��180�㣭(��PAB����PBA)��90�㣻
��APƽ�֡�DAB��
���DAP����PAB��
��AB��CD...
24
��������������������ı���ABCD��ƽ���ı��Σ�
��AD��CB��AB��CD��
���DAB����CBA��180�㣬
�֡�AP��BP�ֱ�ƽ�֡�DAB�͡�CBA��
���PAB����PBA�� (��DAB����CBA)��90�㣬
�ڡ�APB�У���APB��180�㣭(��PAB����PBA)��90�㣻
��APƽ�֡�DAB��
���DAP����PAB��
��AB��CD... ����ѧϰ�����Ķ����н�����̣�
��һԪ���β���ʽ��x2��5x��0��
��������
��x2��5x=0����ã�x1=0��x2=5����������y=x2��5x��x��Ľ�������Ϊ��0��0���ͣ�5��0�����������κ���y=x2��5x�Ĵ���ͼ����ͼ��ʾ������ͼ���֪����x��0����x��5ʱ����ͼ��λ��x���Ϸ�����ʱy��0����x2��5x��0�����ԣ�һԪ���β���ʽx2��5x��0�Ľ⼯Ϊ��x��0����x��5��
ͨ��������������̵�ѧϰ����������˼·�ͷ�������������⣺
��1��������������У�����������ѧ˼���е��� ������ ������ֻ����ţ�
��ת��˼�� �ڷ�������˼�� �����ν��˼��
��2��һԪ���β���ʽx2��5x��0�Ľ⼯Ϊ�� ��
��3�������Ƶķ�����һԪ���β���ʽ��x2��2x��3��0��
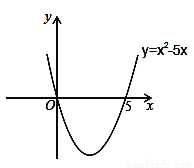
 ��1���٣��ۣ�2��0��x��5��3��x����1����x��3��
�������������������1����������У�����ת��˼������ν��˼�룻
��2���۲�ͼ��д��һԪ���β���ʽ��x2��5x��0�Ľ⼯��
��3�����躯������ʽ������a��ֵȷ�������ߵĿ������ϣ����ҳ���������x���ཻ�����㣬�Ϳ��Ի��������ߣ�����y��0ȷ��һԪ���β���ʽx2��2x��3��0�Ľ⼯��
�����������������
��1������...
��1���٣��ۣ�2��0��x��5��3��x����1����x��3��
�������������������1����������У�����ת��˼������ν��˼�룻
��2���۲�ͼ��д��һԪ���β���ʽ��x2��5x��0�Ľ⼯��
��3�����躯������ʽ������a��ֵȷ�������ߵĿ������ϣ����ҳ���������x���ཻ�����㣬�Ϳ��Ի��������ߣ�����y��0ȷ��һԪ���β���ʽx2��2x��3��0�Ľ⼯��
�����������������
��1������... ��������y=ax2��1ƽ�ƺ���������y=a��x��1��2�غϣ�������y=ax2��1�ϵĵ�A��2��3��ͬʱƽ�Ƶ�A�䣬��ô��A�������Ϊ��������
A. ��3��4�� B. ��1��2�� C. ��3��2�� D. ��1��4��
 A
����������������
��������y=ax2��1�Ķ��������ǣ�0����1����������y=a��x��1��2�Ķ��������ǣ�1��0�����ཫ������y=ax2��1����ƽ��1����λ��������ƽ��1����λ�õ�������y=a��x��1��2���ཫ��A��2��3������ƽ��1����λ��������ƽ��1����λ�õ���A�������Ϊ��3��4����
��ѡA��
A
����������������
��������y=ax2��1�Ķ��������ǣ�0����1����������y=a��x��1��2�Ķ��������ǣ�1��0�����ཫ������y=ax2��1����ƽ��1����λ��������ƽ��1����λ�õ�������y=a��x��1��2���ཫ��A��2��3������ƽ��1����λ��������ƽ��1����λ�õ���A�������Ϊ��3��4����
��ѡA�� ��֪������y��x2��mx��m��2.
(1)��֤����������x�����������㣻
(2)����������x���һ������Ϊ(2��0)����m��ֵ����������x����һ�������꣮
 (1)֤��������(2)��������x����һ��������Ϊ(0��0)
�������������������1����֤����������x����������ͬ�Ľ��㣬ֻҪ֤������0���ɣ�
��2����(2��0)���������߽���ʽ�����ɵõ�m��ֵ���Ӷ��õ������ߵĽ���ʽ����y=0���ⷽ�̼��ɵõ����ۣ�
�����������������
(1)�ߦ���(��m)2��4(m��2)��m2��4m��8��(m��2)2��4��0�� �����������x�����������㣮
...
(1)֤��������(2)��������x����һ��������Ϊ(0��0)
�������������������1����֤����������x����������ͬ�Ľ��㣬ֻҪ֤������0���ɣ�
��2����(2��0)���������߽���ʽ�����ɵõ�m��ֵ���Ӷ��õ������ߵĽ���ʽ����y=0���ⷽ�̼��ɵõ����ۣ�
�����������������
(1)�ߦ���(��m)2��4(m��2)��m2��4m��8��(m��2)2��4��0�� �����������x�����������㣮
... ��֪���κ���y��x2��3x��m(mΪ����)��ͼ����x���һ������Ϊ(1��0)�������x��һԪ���η���x2��3x��m��0����ʵ������( )
A. x1��1��x2����1 B. x1��1��x2��2 C. x1��1��x2��0 D. x1��1��x2��3
 B
���������������������x��һԪ���η���x2-3x+m=0����ʵ�������Ƕ��κ���y=x2-3x+m��mΪ��������ͼ����x�����������ĺ����꣮�߶��κ����Ľ���ʽ��y=x2-3x+m��mΪ����������������ߵĶԳ����ǣ�x=��
�֡߶��κ���y=x2-3x+m��mΪ��������ͼ����x���һ������Ϊ��1��0����
����������ߵĶԳ�����֪������������x�����һ������������ǣ�2��0����
...
B
���������������������x��һԪ���η���x2-3x+m=0����ʵ�������Ƕ��κ���y=x2-3x+m��mΪ��������ͼ����x�����������ĺ����꣮�߶��κ����Ľ���ʽ��y=x2-3x+m��mΪ����������������ߵĶԳ����ǣ�x=��
�֡߶��κ���y=x2-3x+m��mΪ��������ͼ����x���һ������Ϊ��1��0����
����������ߵĶԳ�����֪������������x�����һ������������ǣ�2��0����
... �����Ĵ�����װ��4������3�������5������ÿ�������ɫ��ͬ����������ͬ��������������һ����������__��Ŀ��������
 ��
����������Ϊ��������7������,3�������5������,������������һ����,Ϊ����ĸ�����,����ĸ�����,����ĸ�����,�ɼ���������ĸ������,�ʴ�Ϊ:��.
��
����������Ϊ��������7������,3�������5������,������������һ����,Ϊ����ĸ�����,����ĸ�����,����ĸ�����,�ɼ���������ĸ������,�ʴ�Ϊ:��. ��ͼ����A�ص�C�أ��ɹ�ѡ��ķ�������ˮ·����½·���߿��У���A�ص�B��������ˮ·������½·����B�ص�C����3��½·�ɹ�ѡ���߿��У���A�ز���B��ֱ�ߵ�C�أ����A�ص�C�ؿɹ�ѡ��ķ����У�������

A. 20�� B. 8�� C. 5�� D. 13��
 D
������������ֻ��ֱ�����A��B��B��C��A��C���������ٽ�һ���������㼴�ɣ�
��������
�۲�ͼ�Σ���
A��B��4����B��C��3��������A��B��C��4��3=12����A��Cһ����
���Դ�A�ص�C�ؿɹ�ѡ��ķ�����13����
��ѡD��
D
������������ֻ��ֱ�����A��B��B��C��A��C���������ٽ�һ���������㼴�ɣ�
��������
�۲�ͼ�Σ���
A��B��4����B��C��3��������A��B��C��4��3=12����A��Cһ����
���Դ�A�ص�C�ؿɹ�ѡ��ķ�����13����
��ѡD�� ʩ����Ҫ��һ�������Ϊ�����ߵĹ�·��������߶�Ϊ6�ף�����OMΪ12�ף�����O��Ϊԭ�㣬OM����ֱ��Ϊx�Ὠ��ֱ������ϵ����ͼ��ʾ����
��1��ֱ��д����M�������߶���P�����ꣻ
��2��������������ߵĺ�������ʽ��
��3��ʩ���Ӽƻ��������ſڴһ�����Ρ����ּܡ�ABCD��ʹA��D�����������ϣ�B��C���ڵ���OM�ϣ�Ϊ�˳ﱸ���ϣ�����������ּܡ�����ľ��AB��AD��DC�ij���֮�͵����ֵ�Ƕ��٣������ʩ���Ӽ���һ�£�
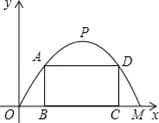
 ��1��M��12��0����P��6��6������2��y=x2+2x����3��15�ף�
�����������������ȷ���������ߵĶ���ʽ�������������ߵĶ���ʽ���ֹ�ԭ�㣨0��0�����Ϳ���ȷ�������߽���ʽ����OB=x���ɶԳ��Ե�CM=x�������Ϳ����ú�x��ʽ�ӱ�ʾAB��AD��CD�ˣ�Ϊ������ľ��AB��AD��DC�ij���֮�͵����ֵ���ṩ���ݣ�
�����������1��M��12��0����P��6��6��
��2���߶������꣨...
��1��M��12��0����P��6��6������2��y=x2+2x����3��15�ף�
�����������������ȷ���������ߵĶ���ʽ�������������ߵĶ���ʽ���ֹ�ԭ�㣨0��0�����Ϳ���ȷ�������߽���ʽ����OB=x���ɶԳ��Ե�CM=x�������Ϳ����ú�x��ʽ�ӱ�ʾAB��AD��CD�ˣ�Ϊ������ľ��AB��AD��DC�ij���֮�͵����ֵ���ṩ���ݣ�
�����������1��M��12��0����P��6��6��
��2���߶������꣨... 
