��Ŀ����
������y=��x2+bx+c�ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���ʾ��
x | �� | ��2 | ��1 | 0 | 1 | 2 | �� |
y | �� | 0 | 4 | 6 | 6 | 4 | �� |
���ϱ���֪������˵���У�������ǣ�������
A. ��������x���һ����������Ϊ����2��0�� B. ��������y��Ľ�������Ϊ��0��6��
C. �����ߵĶԳ�����ֱ��x=0 D. �������ڶԳ�����ಿ����������
 C
����������������
��x=��2ʱ��y=0���������߹�����2��0��������������x���һ����������Ϊ����2��0������A��ȷ��
��x=0ʱ��y=6������������y��Ľ�������Ϊ��0��6������B��ȷ��
��x=0��x=1ʱ��y=6����Գ���Ϊx=����C����
��x��ʱ��y��x������������������ڶԳ�����ಿ���������ģ���D��ȷ��
��ѡC��
C
����������������
��x=��2ʱ��y=0���������߹�����2��0��������������x���һ����������Ϊ����2��0������A��ȷ��
��x=0ʱ��y=6������������y��Ľ�������Ϊ��0��6������B��ȷ��
��x=0��x=1ʱ��y=6����Գ���Ϊx=����C����
��x��ʱ��y��x������������������ڶԳ�����ಿ���������ģ���D��ȷ��
��ѡC��
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д���ͼ����?ABCD�У�AB��6��BC��8����BCD��ƽ���߽�AD�ڵ�E����BA���ӳ����ڵ�F����AE��AF��ֵ����(�� ��)
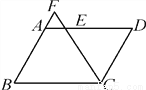
A. 2 B. 3 C. 4 D. 6
 C
�������������������ƽ���ı��ε����ʺͽ�ƽ���ߵó���F=��FCB��֤��BF=BC=8��ͬ����DE=CD=6�����AF=BF��AB=2��AE=AD��DE=2�����ɵó���������ı���ABCD��ƽ���ı��Σ� ��AB��CD��AD=BC=8��CD=AB=6��
���F=��DCF���ߡ�Cƽ����ΪCF�����FCB=��DCF�����F=��FCB�� ��BF=BC=8��
ͬ����DE=CD=6�� ��A...
C
�������������������ƽ���ı��ε����ʺͽ�ƽ���ߵó���F=��FCB��֤��BF=BC=8��ͬ����DE=CD=6�����AF=BF��AB=2��AE=AD��DE=2�����ɵó���������ı���ABCD��ƽ���ı��Σ� ��AB��CD��AD=BC=8��CD=AB=6��
���F=��DCF���ߡ�Cƽ����ΪCF�����FCB=��DCF�����F=��FCB�� ��BF=BC=8��
ͬ����DE=CD=6�� ��A... ��2016�㽭ʡ�����У���ֱ֪������ϵ�����ĸ���O��0��0����A��3��0����B��1��1����C��x��1��������O��A��B��CΪ������ı�����ƽ���ı��Σ���x=____________��
 4��2��
������������������������⻭ͼ���£�
��O��A��B��CΪ������ı�����ƽ���ı��Σ���C��4��1����2��1������x=4��2���ʴ�Ϊ��4��2��
4��2��
������������������������⻭ͼ���£�
��O��A��B��CΪ������ı�����ƽ���ı��Σ���C��4��1����2��1������x=4��2���ʴ�Ϊ��4��2�� ����ѧϰ�����Ķ����н�����̣�
��һԪ���β���ʽ��x2��5x��0��
��������
��x2��5x=0����ã�x1=0��x2=5����������y=x2��5x��x��Ľ�������Ϊ��0��0���ͣ�5��0�����������κ���y=x2��5x�Ĵ���ͼ����ͼ��ʾ������ͼ���֪����x��0����x��5ʱ����ͼ��λ��x���Ϸ�����ʱy��0����x2��5x��0�����ԣ�һԪ���β���ʽx2��5x��0�Ľ⼯Ϊ��x��0����x��5��
ͨ��������������̵�ѧϰ����������˼·�ͷ�������������⣺
��1��������������У�����������ѧ˼���е��� ������ ������ֻ����ţ�
��ת��˼�� �ڷ�������˼�� �����ν��˼��
��2��һԪ���β���ʽx2��5x��0�Ľ⼯Ϊ�� ��
��3�������Ƶķ�����һԪ���β���ʽ��x2��2x��3��0��
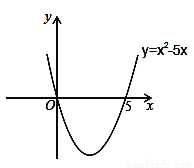
 ��1���٣��ۣ�2��0��x��5��3��x����1����x��3��
�������������������1����������У�����ת��˼������ν��˼�룻
��2���۲�ͼ��д��һԪ���β���ʽ��x2��5x��0�Ľ⼯��
��3�����躯������ʽ������a��ֵȷ�������ߵĿ������ϣ����ҳ���������x���ཻ�����㣬�Ϳ��Ի��������ߣ�����y��0ȷ��һԪ���β���ʽx2��2x��3��0�Ľ⼯��
�����������������
��1������...
��1���٣��ۣ�2��0��x��5��3��x����1����x��3��
�������������������1����������У�����ת��˼������ν��˼�룻
��2���۲�ͼ��д��һԪ���β���ʽ��x2��5x��0�Ľ⼯��
��3�����躯������ʽ������a��ֵȷ�������ߵĿ������ϣ����ҳ���������x���ཻ�����㣬�Ϳ��Ի��������ߣ�����y��0ȷ��һԪ���β���ʽx2��2x��3��0�Ľ⼯��
�����������������
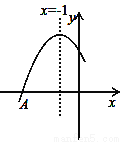
��1������... ��ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣�ͼ�����A����3��0�����Գ���Ϊֱ��x=��1���������½��ۣ���abc��0 ��b2��4ac��0 ��4b+c��0 ����B����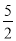 ��y1����C����
��y1����C����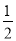 ��y2��Ϊ����ͼ���ϵ����㣬��y1��y2�ݵ���3��x��1ʱ��y��0��
��y2��Ϊ����ͼ���ϵ����㣬��y1��y2�ݵ���3��x��1ʱ��y��0��
������ȷ�Ľ����ǣ���д������ȷ���۵���ţ�__________________��
 �ڢۢ�
����������������
��ͼ���֪��a��0��b��0��c��0����abc��0���ʢٴ���
����������x�����������㣬��b2��4ac��0���ʢ���ȷ��
�������߶Գ���Ϊx=��1����x�ύ��A����3��0��������������x�����һ������Ϊ��1��0������a+b+c=0���� =��1����b=2a��c=��3a����4b+c=8a��3a=5a��0���ʢ���ȷ��
��B������y1����C������y2����...
�ڢۢ�
����������������
��ͼ���֪��a��0��b��0��c��0����abc��0���ʢٴ���
����������x�����������㣬��b2��4ac��0���ʢ���ȷ��
�������߶Գ���Ϊx=��1����x�ύ��A����3��0��������������x�����һ������Ϊ��1��0������a+b+c=0���� =��1����b=2a��c=��3a����4b+c=8a��3a=5a��0���ʢ���ȷ��
��B������y1����C������y2��Ϊ��... ��������y=ax2��1ƽ�ƺ���������y=a��x��1��2�غϣ�������y=ax2��1�ϵĵ�A��2��3��ͬʱƽ�Ƶ�A�䣬��ô��A�������Ϊ��������
A. ��3��4�� B. ��1��2�� C. ��3��2�� D. ��1��4��
 A
����������������
��������y=ax2��1�Ķ��������ǣ�0����1����������y=a��x��1��2�Ķ��������ǣ�1��0�����ཫ������y=ax2��1����ƽ��1����λ��������ƽ��1����λ�õ�������y=a��x��1��2���ཫ��A��2��3������ƽ��1����λ��������ƽ��1����λ�õ���A�������Ϊ��3��4����
��ѡA��
A
����������������
��������y=ax2��1�Ķ��������ǣ�0����1����������y=a��x��1��2�Ķ��������ǣ�1��0�����ཫ������y=ax2��1����ƽ��1����λ��������ƽ��1����λ�õ�������y=a��x��1��2���ཫ��A��2��3������ƽ��1����λ��������ƽ��1����λ�õ���A�������Ϊ��3��4����
��ѡA�� ��֪������y��x2��mx��m��2.
(1)��֤����������x�����������㣻
(2)����������x���һ������Ϊ(2��0)����m��ֵ����������x����һ�������꣮
 (1)֤��������(2)��������x����һ��������Ϊ(0��0)
�������������������1����֤����������x����������ͬ�Ľ��㣬ֻҪ֤������0���ɣ�
��2����(2��0)���������߽���ʽ�����ɵõ�m��ֵ���Ӷ��õ������ߵĽ���ʽ����y=0���ⷽ�̼��ɵõ����ۣ�
�����������������
(1)�ߦ���(��m)2��4(m��2)��m2��4m��8��(m��2)2��4��0�� �����������x�����������㣮
...
(1)֤��������(2)��������x����һ��������Ϊ(0��0)
�������������������1����֤����������x����������ͬ�Ľ��㣬ֻҪ֤������0���ɣ�
��2����(2��0)���������߽���ʽ�����ɵõ�m��ֵ���Ӷ��õ������ߵĽ���ʽ����y=0���ⷽ�̼��ɵõ����ۣ�
�����������������
(1)�ߦ���(��m)2��4(m��2)��m2��4m��8��(m��2)2��4��0�� �����������x�����������㣮
... �����Ĵ�����װ��4������3�������5������ÿ�������ɫ��ͬ����������ͬ��������������һ����������__��Ŀ��������
 ��
����������Ϊ��������7������,3�������5������,������������һ����,Ϊ����ĸ�����,����ĸ�����,����ĸ�����,�ɼ���������ĸ������,�ʴ�Ϊ:��.
��
����������Ϊ��������7������,3�������5������,������������һ����,Ϊ����ĸ�����,����ĸ�����,����ĸ�����,�ɼ���������ĸ������,�ʴ�Ϊ:��. ��ͼ����ABO�У�AB��OB��OB= ��AB=1���ѡ�ABO�Ƶ�O��ת150���õ���A1B1O�����A1������Ϊ
��AB=1���ѡ�ABO�Ƶ�O��ת150���õ���A1B1O�����A1������Ϊ
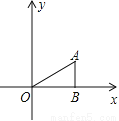
A. ����1�� 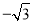 �� B. ����1��
�� B. ����1�� 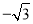 ����2��0�� C. ��
����2��0�� C. �� ����1����0����2�� D. ��
����1����0����2�� D. ��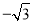 ����1��
����1��
 B
�������������������Ҫ�������ۣ��ڰѡ�ABO�Ƶ�O˳ʱ����ת150�����ʱ����ת150���õ���A1B1Oʱ��A1�����꣬����
�ߡ�ABO�У�AB��OB��OB=��AB=1��
��tan��AOB=��
���AOB=30�㣮
��ͼ1������ABO�Ƶ�O˳ʱ����ת150���õ���A1B1O��
���A1OC=150�㩁��AOB����BOC=150�㩁30�㩁90��=30�㣬...
B
�������������������Ҫ�������ۣ��ڰѡ�ABO�Ƶ�O˳ʱ����ת150�����ʱ����ת150���õ���A1B1Oʱ��A1�����꣬����
�ߡ�ABO�У�AB��OB��OB=��AB=1��
��tan��AOB=��
���AOB=30�㣮
��ͼ1������ABO�Ƶ�O˳ʱ����ת150���õ���A1B1O��
���A1OC=150�㩁��AOB����BOC=150�㩁30�㩁90��=30�㣬... 
