��Ŀ����
9��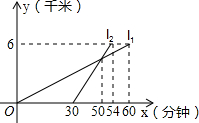 ijУ���꼶��ѧ������ѧУ6ǧ�Ľ������Σ�һ����ѧ�����У���һ����ѧ�������г�����ͬ��·ǰ������ͼ��l1��l2�ֱ��ʾ���к��ﳵ��ѧ��ǰ��Ŀ�ĵ����ߵ�·��y��ǧ�ף������õ�ʱ��x�����ӣ�֮��ĺ���ͼ���������жϣ�
ijУ���꼶��ѧ������ѧУ6ǧ�Ľ������Σ�һ����ѧ�����У���һ����ѧ�������г�����ͬ��·ǰ������ͼ��l1��l2�ֱ��ʾ���к��ﳵ��ѧ��ǰ��Ŀ�ĵ����ߵ�·��y��ǧ�ף������õ�ʱ��x�����ӣ�֮��ĺ���ͼ���������жϣ����ﳵ��ѧѧ�Ȳ��е�ѧ��������30���ӣ�
�ڲ��е��ٶ���ÿСʱ6ǧ�ף�
���ﳵ��ѧ���ӳ������ϲ��е�ѧ������20���ӣ�
���ﳵ��ѧ���Ͳ��е�ѧ��ͬʱ����Ŀ�ĵأ�
����ȷ���ж���3����
���� ���ݺ���ͼ�����жϢ٢ڢۢ��Ƿ���ȷ��������Խ����
��� �⣺�ɺ���ͼ���֪��
�ﳵ��ѧ���Ȳ��е�ѧ��������30���ӣ��ʢ���ȷ��
���е��ٶ��ǣ�$6��\frac{60}{60}=6$ǧ��/Сʱ���ʢ���ȷ��
�ﳵ��ѧ���ӳ������ϲ��е�ѧ������20���ӣ��ʢ���ȷ��
�ﳵ��ѧ���ȵ���Ŀ�ĵأ��ʢܴ���
����ȷ���ж���3����
�ʴ�Ϊ��3��
���� ���⿼��һ�κ�����Ӧ�ã�����Ĺؼ�����ȷ���⣬�������ν�ϵ�˼�������⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
19������˵����ȷ���ǣ�������
| A�� | x-1������x��1 | B�� | $\frac{m+n}{3}$��$\frac{xy}{2}$���ǵ���ʽ | ||
| C�� | 0��x2+xy+y2���Ƕ���ʽ | D�� | a��-6��abc��$\frac{2x-1}{5}$������ʽ |
20�����и�ʽ������ȷ���ǣ�������
| A�� | 2x4-x2=x2 | B�� | ��2x2��4=8x8 | C�� | x2•x3=x6 | D�� | ��-x��6�£�-x��2=x4 |
14�����������У���ȷ���ǣ�������
| A�� | ���εĶԽ����ഹֱ��ƽ�� | B�� | ƽ���ı��εĶԽ������ | ||
| C�� | ���εĶԽ����ഹֱ | D�� | ���εĶԽ������ |
18�����й���x�ķ��̣�һ����һԪ���η��̵��ǣ�������
| A�� | ax2-5x+3=0 | B�� | 2x4=5x2 | C�� | ${x^2}+\frac{x^2}{x}=1$ | D�� | $\frac{1}{2}{x^2}+\sqrt{3}x-4=0$ |






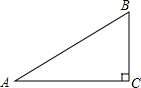 ��ͼ����ABC�У���C=90�㣬С��ͬѧ����һ��Բ����A��C���㣬���Ҹ�Բ��Բ�ĵ�AB��AC������ȣ��������ó߹���ͼ�İ취����С��ͬѧȷ��Բ��D������д������������ͼ�ۼ�����
��ͼ����ABC�У���C=90�㣬С��ͬѧ����һ��Բ����A��C���㣬���Ҹ�Բ��Բ�ĵ�AB��AC������ȣ��������ó߹���ͼ�İ취����С��ͬѧȷ��Բ��D������д������������ͼ�ۼ�����