题目内容
18．
如图，平行四边形ABCD的对角线交于点O，且AB=6，△OCD的周长为27，则平行四边形ABCD的两条对角线的和是42．
分析 首先由平行四边形的性质可求出CD的长，由条件△OCD的周长为27，即可求出OD+OC的长，再根据平行四边的对角线互相平分即可求出平行四边形的两条对角线的和．
解答 解：∵四边形ABCD是平行四边形，
∴AB=CD=6，
∵△OCD的周长为27，
∴OD+OC=27-6=21，
∵BD=2DO，AC=2OC，
∴平行四边形ABCD的两条对角线的和=BD+AC=2（DO+OC）=42，
故答案为：42．
点评 本题主要考查了平行四边形的基本性质，并利用性质解题．熟记平行四边形的性质，由三角形的周长求出OD+OC是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
8．
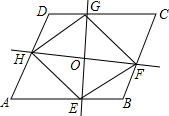如图，过?ABCD的对角线AC的中点O任作两条互相垂直的直线，分别交AB，BC，CD，DA于E，F，G，H四点，连接EF，FG，GH，HE，有下面四个结论，①OH=OF；②∠HGE=∠FGE；③S四边形DHOG=S四边形BFOE；④△AHO≌△AEO，其中正确的是（ ）
如图，过?ABCD的对角线AC的中点O任作两条互相垂直的直线，分别交AB，BC，CD，DA于E，F，G，H四点，连接EF，FG，GH，HE，有下面四个结论，①OH=OF；②∠HGE=∠FGE；③S四边形DHOG=S四边形BFOE；④△AHO≌△AEO，其中正确的是（ ）| A． | ①③ | B． | ①②③ | C． | ②④ | D． | ②③④ |
13．2016年2月20日，河南宝丰县中华曲艺展览馆前空旷的麦田里，来自全国各地的民间艺人们支好大鼓、调试好二胡、架上喇叭等家伙什准备开唱，“真可谓一日能听千台戏，三天看破万卷书”．据统计有23万人参加这次盛会，23万用科学记数法表示为（ ）
| A． | 2.3×104 | B． | 2.3×105 | C． | 2.3×106 | D． | 23×105 |
3．下列式子化简后，与$\sqrt{2}$不能合并的是（ ）
| A． | $\sqrt{8}$ | B． | $\sqrt{\frac{1}{2}}$ | C． | $\sqrt{12}$ | D． | $\sqrt{18}$ |
10．下列运算正确的是（ ）
| A． | （-3mn）2=-6m2n2 | B． | 4x4+2x4+x4=6x4 | C． | （a-b）（-a-b）=a2-b2 | D． | （xy）2÷（-xy）=-xy |