题目内容
15.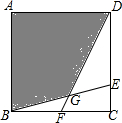 如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )
如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )| A. | $\frac{9}{14}$ | B. | $\frac{2}{3}$ | C. | $\frac{7}{10}$ | D. | $\frac{3}{4}$ |
分析 过点E作EH∥FG.由DE=2CE,BF=FC可知FC=FB=$\frac{1}{2}$,EC=$\frac{1}{3}$,可求得△DFC的面积=$\frac{1}{4}$,由EH∥DF,可得到BF:BH=3:5,根据相似三角形的面积比等于相似比的平方可求得△BHE的面积=$\frac{5}{36}$,最后根据阴影部分的面积=正方形的面积-△BGF的面积-△DFC的面积计算即可.
解答 解:如图所示,过点E作EH∥FG.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=1.
∵DE=2CE,BF=FC,
∴FC=FB=$\frac{1}{2}$,EC=$\frac{1}{3}DC=\frac{1}{3}×1$=$\frac{1}{3}$.
∴${S}_{△DFC}=\frac{1}{2}×\frac{1}{2}×1$=$\frac{1}{4}$.
∵EH∥DF,
∴$\frac{HC}{FC}=\frac{EC}{CD}=\frac{1}{3}$.
∴$HC=\frac{1}{3}FC=\frac{1}{3}×\frac{1}{2}$=$\frac{1}{6}$.
∴BH=$\frac{5}{6}$.
∴BF:BH=3:5.
∴${S}_{△BHE}=\frac{1}{2}BH•EC=\frac{1}{2}×\frac{5}{6}×\frac{1}{3}$=$\frac{5}{36}$.
∵GF∥EH,
∴△BFG的面积:△BEH的面积=9:25.
∴△BFG的面积:$\frac{5}{36}$=9:25.
∴△BFG的面积=$\frac{1}{20}$.
∴阴影部分的面积=正方形的面积-△BGF的面积-△DFC的面积=1-$\frac{1}{20}$-$\frac{1}{4}$=$\frac{7}{10}$.
故选:C.
点评 本题主要考查的是相似三角形的性质和判定、正方形的性质、三角形的面积公式,利用相似三角形的性质求得△BFG的面积是解题的关键.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | y=-2x2-12x+19 | B. | y=-2x2+12x-19 | C. | y=-2x2+12x-17 | D. | y=-2x2-12x-17 |
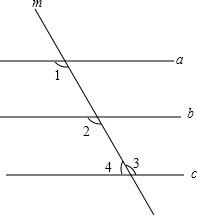 如图,直线a,b,c被直线m所截,量得∠1=∠2=∠3.
如图,直线a,b,c被直线m所截,量得∠1=∠2=∠3.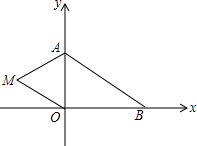 如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.
如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.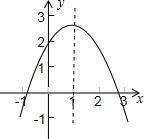 已知二次函数y=ax2+bx+c的图象如图所示,下列说法①a>0;②b2-4ac>0;③4a+2b+c>0;④c<0;⑤b>0.其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,下列说法①a>0;②b2-4ac>0;③4a+2b+c>0;④c<0;⑤b>0.其中正确的有( )
 如图,△ABC中,CD是∠ACB的角平分线,若∠A=30°,∠B=60°,则∠DCB=45°.
如图,△ABC中,CD是∠ACB的角平分线,若∠A=30°,∠B=60°,则∠DCB=45°.