题目内容
10.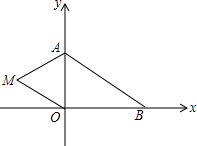 如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.
如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.(1)求a,b的值;
(2)如果在第二象限内有一点M(m,1),请用含m的式子表示四边形ABOM的面积;
(3)在(2)条件下,当m=-$\frac{3}{2}$时,在坐标轴的负半轴上是否存在点N,使得四边形ABOM的面积与△ABN的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
分析 (1)根据非负数的性质得到a-2=0,b-3=0,解方程即可得到a,b的值;
(2)过点M作MN丄y轴于点N.根据四边形AMOB面积=S△AMO+S△AOB求解即可;
(3)当m=-$\frac{3}{2}$时,四边形ABOM的面积=4.5,可得S△ABN=4.5,再分两种情况:①当N在x负半轴上时,②当N在y负半轴上时,进行讨论得到点N的坐标.
解答 解:(1)∵a,b满足|a-2|+(b-3)2=0,
∴a-2=0,b-3=0,
解得a=2,b=3.
故a的值是2,b的值是3;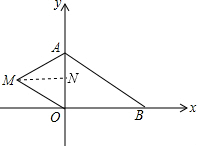 (2)过点M作MN丄y轴于点N.
(2)过点M作MN丄y轴于点N.
四边形AMOB面积=S△AMO+S△AOB
=$\frac{1}{2}$MN•OA+$\frac{1}{2}$OA•OB
=$\frac{1}{2}$×(-m)×2+$\frac{1}{2}$×2×3
=-m+3;
(3)当m=-$\frac{3}{2}$时,四边形ABOM的面积=4.5.
∴S△ABN=4.5,
①当N在x轴负半轴上时,
设N(x,0),则
S△ABN=$\frac{1}{2}$AO•NB=$\frac{1}{2}$×2×(3-x)=4.5,
解得x=-1.5;
②当N在y轴负半轴上时,
设N(0,y),则
S△ABN=$\frac{1}{2}$BO•AN=$\frac{1}{2}$×3×(2-y)=4.5,
解得y=-1.
∴N(0,-1)或N(-1.5,0).
点评 考查了坐标与图形性质,非负数的性质,三角形的面积,关键是求得a,b的值,其中(3)中注意分类思想和数形结合思想的应用.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
15.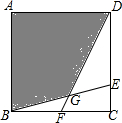 如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )
如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )
 如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )
如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )| A. | $\frac{9}{14}$ | B. | $\frac{2}{3}$ | C. | $\frac{7}{10}$ | D. | $\frac{3}{4}$ |
2. 如图,平行四边形ABCD的周长为16cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
如图,平行四边形ABCD的周长为16cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
 如图,平行四边形ABCD的周长为16cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
如图,平行四边形ABCD的周长为16cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
20.下列计算中,正确的是( )
| A. | x3•x2=x6 | B. | 3x2-2x2=x2 | C. | (x2)3=x5 | D. | $\sqrt{4}$=±2 |
 如图,在Rt△ABC中,∠BAC=90°,如果∠A=30°,D为AB的中点,BC=3cm,则CD=3cm.
如图,在Rt△ABC中,∠BAC=90°,如果∠A=30°,D为AB的中点,BC=3cm,则CD=3cm. 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点C是线段AB上一点,四边形OADC是菱形,则OD的长=4.8.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点C是线段AB上一点,四边形OADC是菱形,则OD的长=4.8.