题目内容
4．
如图，△ABC中，CD是∠ACB的角平分线，若∠A=30°，∠B=60°，则∠DCB=45°．
分析 先根据三角形内角和定理得到∠ACB的度数，再根据角平分线的性质即可求解．
解答 解：∵△ABC中，∠A=30°，∠B=60°，
∴∠ACB=180°-30°-60°=90°，
∵CD是∠ACB的角平分线，
∴∠DCB=45°．
故答案为：45°．
点评 考查了三角形内角和定理和角平分线的性质，本题根据三角形的内角和等于180°求解，是基础题，准确识别图形是解题的关键．
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
14．下列调查中，适宜采用全面调查方式的是（ ）
| A． | 调查初三某班体育模拟考试成绩的满分率 | |
| B． | 调查某类烟花爆竹燃放安全情况 | |
| C． | 调查某品牌牛奶的质量合格情况 | |
| D． | 调查全国中学生对“雾霾”的了解情况 |
15．
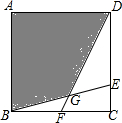如图，在正方形ABCD中，E在CD边上，F在BC边上，AB=1，DE=2CE，BF=FC，BE与DF交于点G，则图中阴影部分（即四边形ABGD）的面积是（ ）
如图，在正方形ABCD中，E在CD边上，F在BC边上，AB=1，DE=2CE，BF=FC，BE与DF交于点G，则图中阴影部分（即四边形ABGD）的面积是（ ）| A． | $\frac{9}{14}$ | B． | $\frac{2}{3}$ | C． | $\frac{7}{10}$ | D． | $\frac{3}{4}$ |
矩形ABCD中，E在CD上，将△ADE沿AE折叠，使点D落在边BC上的F处，如果∠EAD=15°，则∠BAF为60°．
如图，直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A，B，点C是线段AB上一点，四边形OADC是菱形，则OD的长=4.8．
9．
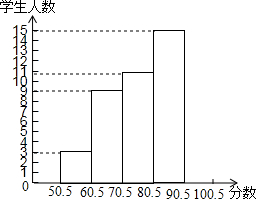为了了解奥运知识，某中学举行了一次“奥运知识竞赛”，共有900名学生参加了这次竞赛，为了了解本次竞赛情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分），进行统计，请你根据下面尚未完成的统计表和统计图，解答下列问题．
（1）根据以上信息，统计表中A=0.18，B=12，C=0.24；
（2）补全统计图；
（3）在该问题中，个体是每一个学生的竞赛成绩；
（4）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？
为了了解奥运知识，某中学举行了一次“奥运知识竞赛”，共有900名学生参加了这次竞赛，为了了解本次竞赛情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分），进行统计，请你根据下面尚未完成的统计表和统计图，解答下列问题．| 分组 | 频数 | 频率 |
| 50.5～60.5 | 3 | 0.06 |
| 60.5～70.5 | 9 | A |
| 70.5～80.5 | 11 | 0.22 |
| 80.5～90.5 | 15 | 0.30 |
| 90.5～100.5 | B | C |
（2）补全统计图；
（3）在该问题中，个体是每一个学生的竞赛成绩；
（4）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？
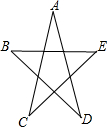如图，∠A+∠B+∠C+∠D+∠E的度数是180°．
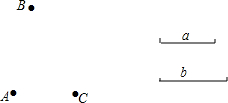如图，已知平面上三个点A，B，C和线段a，b，按下列要求画图．