题目内容
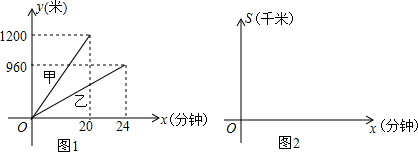
7.A,B,C三地依次在一条直线公路上,甲,乙二人同时从A,B两地出发沿公路匀速步行到C地,两人离出发地的距离y(米)与出发时间x(分钟)函数图象如图1所示.(1)甲的步行速度为60米/分钟,乙的步行速度为40米/分钟,A,B两地之间的距离为240米.
(2)设两人离B地的距离为s(米),出发时间x(分钟),请在图(2)中分别画出甲,乙二人s与x的函数图象.
(3)两人出发多长时间在途中相遇?
分析 (1)根据速度=路程÷时间就可以求出甲、乙的速度,由图象信息可以得出AC,BC的距离,由AB-BC即可求得A,B两地之间的距离;
(2)先用(1)的结论求出甲走到B地的时间,从而可以画出大致图形;
(3)分别求出解析式,再构成方程组求出其解就可以得出结论.
解答 解:(1)甲的步行速度为:1200÷20=60(米/分钟);
乙的步行速度为960÷24=40(米/分钟);
A,B两地之间的距离为:1200-960=240(米);
故答案为60,40,240;
(2)甲由A到B的时间:240÷60=4(分)
甲,乙二人s与x的函数图象如图: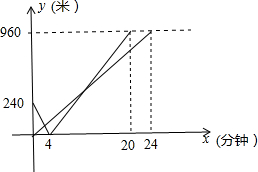
(3)甲经过(4,0)(20,960)设解析式为s1=kx+b
$\left\{\begin{array}{l}{4k+b=0}\\{20k+b=960}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=60}\\{b=-240}\end{array}\right.$,
∴s1=60x-240,
乙经过(0,0),(24,960)设解析式为s2=mx,
∴960=24m,解得m=40,
∴s2=40x,
解40x=60x-240,得x=12,
∴两人出发12分钟在途中相遇.
答:两人出发12分钟在途中相遇.
点评 本题考查了速度=路程÷时间的运用,待定系数法求函数的解析式的运用,由点的坐标画函数图象的运用,一次函数与二元一次方程组的运用.解答时求出一次函数的解析式是关键.

练习册系列答案
相关题目
15.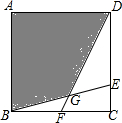 如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )
如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )
 如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )
如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )| A. | $\frac{9}{14}$ | B. | $\frac{2}{3}$ | C. | $\frac{7}{10}$ | D. | $\frac{3}{4}$ |
2. 如图,平行四边形ABCD的周长为16cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
如图,平行四边形ABCD的周长为16cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
 如图,平行四边形ABCD的周长为16cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
如图,平行四边形ABCD的周长为16cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
 矩形ABCD中,E在CD上,将△ADE沿AE折叠,使点D落在边BC上的F处,如果∠EAD=15°,则∠BAF为60°.
矩形ABCD中,E在CD上,将△ADE沿AE折叠,使点D落在边BC上的F处,如果∠EAD=15°,则∠BAF为60°. 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点C是线段AB上一点,四边形OADC是菱形,则OD的长=4.8.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点C是线段AB上一点,四边形OADC是菱形,则OD的长=4.8.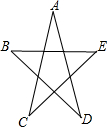 如图,∠A+∠B+∠C+∠D+∠E的度数是180°.
如图,∠A+∠B+∠C+∠D+∠E的度数是180°.