题目内容
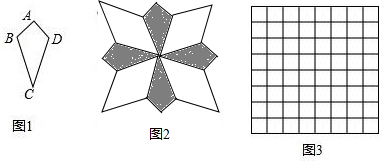
15.实践与探索:定义:两组邻边分别相等,且对边不相等的四边形称为筝形,如图1,四边形ABCD是筝形,其中AB=AD,CB=CD,且AB≠CD.
(1)①命题“菱形是筝形”是假命题(填“真”或“假”);
②请说出筝形和菱形的相同点和不同点(各两条);
(2)请仿照图2的画法,在图3所示的8×8网格中重新设计一个由四个全等的筝形和四个全等的菱形组成的新图案,具体要求如下:
①筝形和菱形顶点都在格点上;
②所设计的图案既是轴对称图形又是中心对称图形,与原图案不能是放大或缩小的关系;
③将新图案中的四个筝形都涂上阴影(建议用一系列平行四边形斜线表示阴影).
分析 (1)①根据筝形定义进行分析即可;
②根据菱形的性质和筝形的性质进行比较;
(2)直接利用轴对称图形以及中心对称图形的性质进而得出符合题意的图形.
解答 解:(1)①命题“菱形是筝形”是假命题;
②筝形和菱形的相同点:两组邻边相等,对角线互相垂直;
不同点:菱形四边相等,筝形只两组邻边分别相等;菱形对角相等,筝形对角不相等;
(2)如图所示: .
.
点评 此题主要考查了利用轴对称设计图案,正确掌握轴对称图形以及中心对称图形的性质是解题关键.

练习册系列答案
相关题目
5.使代数式$\frac{3}{x-3}$有意义的x的取值范围是( )
| A. | x>3 | B. | x=3 | C. | x<3 | D. | x≠3 |
6.下列各点中,在函数y=-$\frac{12}{x}$的图象上的点是( )
| A. | (-2,6) | B. | (-2,-6) | C. | (3,4) | D. | (-3,-4) |
10. 如图,矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为D′,若D′落在∠ABC的平分线上时,DE的长为( )
如图,矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为D′,若D′落在∠ABC的平分线上时,DE的长为( )
 如图,矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为D′,若D′落在∠ABC的平分线上时,DE的长为( )
如图,矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为D′,若D′落在∠ABC的平分线上时,DE的长为( )| A. | 3或4 | B. | $\frac{5}{2}$或$\frac{5}{3}$ | C. | $\frac{5}{2}$或$\frac{3}{5}$ | D. | $\frac{2}{5}$或$\frac{5}{3}$ |
7.下列命题是真命题的是( )
| A. | 如果两角是同位角,那么这两角一定相等 | |
| B. | 两互补的角一定是邻补角 | |
| C. | 如果a2=b2,那么a=b | |
| D. | 如果两个角不相等,那么这两个角不是对顶角 |
4.甲、乙、丙、丁四名射手在预选赛中所得的平均环数$\overline{x}$及其方差s2如表所示,则选拔 一名参赛的人选,应是( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 7 | 8 | 8 | 7 |
| s2 | 6.3 | 6.3 | 7 | 8.7 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
 如图,在平面直角坐标系中,点A在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,点B在y轴上,且AO=AB,若△ABO的面积为12,则k的值为-12.
如图,在平面直角坐标系中,点A在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,点B在y轴上,且AO=AB,若△ABO的面积为12,则k的值为-12. 将一副三角尺按如图所示放置在坐标系内,反比例函数y=$\frac{k}{x}$的图象经过直角顶点A,且交AB边于点C,已知点C的横坐标比点A的横坐标大4.
将一副三角尺按如图所示放置在坐标系内,反比例函数y=$\frac{k}{x}$的图象经过直角顶点A,且交AB边于点C,已知点C的横坐标比点A的横坐标大4. 如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连结AC交NP于Q,连结MQ.
如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连结AC交NP于Q,连结MQ.