题目内容
 如图,已知AP平分∠BAC,DP平分∠CDB,∠C=50°,∠B=20°,则∠P的度数为( )
如图,已知AP平分∠BAC,DP平分∠CDB,∠C=50°,∠B=20°,则∠P的度数为( )| A、10° | B、15° |
| C、30° | D、40° |
考点:三角形内角和定理,三角形的外角性质
专题:
分析:延长BD交AC于E,根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义表示出∠CDP,然后根据三角形的内角和定理列式∠P+∠CDP=∠CAP+∠C,整理即可得解.
解答: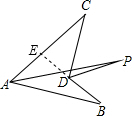 解:如图,延长BD交AC于E,
解:如图,延长BD交AC于E,
由三角形的外角性质得,∠BDC=∠BAC+∠B+∠C=∠BAC+50°+20°=∠BAC+70°,
∵DP平分∠CDB,
∴∠CDP=
∠BAC=
∠BAC+35°,
∵AP平分∠BAC,
∴∠CAP=
∠BAC,
由三角形的内角和定理,∠P+∠CDP=∠CAP+∠C,
∴∠P+
∠BAC+35°=
∠BAC+∠C,
∴∠P=∠C-35°=50°-35°=15°.
故选B.
 解:如图,延长BD交AC于E,
解:如图,延长BD交AC于E,由三角形的外角性质得,∠BDC=∠BAC+∠B+∠C=∠BAC+50°+20°=∠BAC+70°,
∵DP平分∠CDB,
∴∠CDP=
| 1 |
| 2 |
| 1 |
| 2 |
∵AP平分∠BAC,
∴∠CAP=
| 1 |
| 2 |
由三角形的内角和定理,∠P+∠CDP=∠CAP+∠C,
∴∠P+
| 1 |
| 2 |
| 1 |
| 2 |
∴∠P=∠C-35°=50°-35°=15°.
故选B.
点评:本题考查了三角形的内角和定理,三角形的外角性质,熟记定理与性质是解题的关键,难点在于作出辅助线是解题的关键.

练习册系列答案
相关题目
抛物线y=3(x+1)2-2的对称轴是( )
| A、直线x=-2 |
| B、直线x=2 |
| C、直线x=-1 |
| D、直线x=1 |
在下列各数:0.51525354…,
,0.2,
,
,
中,无理数的个数是( )
| 49 |
| 100 |
| 7 |
| 131 |
| 11 |
| 3 | 27 |
| A、2个 | B、3个 | C、4个 | D、5个 |
为了了解我校七年级900名学生的视力情况,李老师从中抽查了80名学生的视力情况.针对这个问题,下面说法正确的是( )
| A、900名学生是总体 |
| B、每名学生是个体 |
| C、80名学生是所抽取的一个样本 |
| D、样本容量是80 |
 已知,如图,MN∥EH,AB∥CD,∠1=110°,求∠2的度数.
已知,如图,MN∥EH,AB∥CD,∠1=110°,求∠2的度数. 如图,直线OC,BC的函数关系式分别是y1=x和y2=-x+6,两直线的交点为C.
如图,直线OC,BC的函数关系式分别是y1=x和y2=-x+6,两直线的交点为C.