题目内容
4.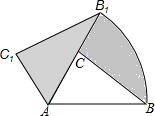 如图,在△ACB中,∠BAC=50°,AC=2,AB=3,现将△ACB绕点A逆时针旋转50°得到△AC1B1,则阴影部分的面积为$\frac{5}{4}$π.
如图,在△ACB中,∠BAC=50°,AC=2,AB=3,现将△ACB绕点A逆时针旋转50°得到△AC1B1,则阴影部分的面积为$\frac{5}{4}$π.
分析 根据旋转的性质可知${S}_{△ABC}={S}_{△A{B}_{1}{C}_{1}}$,由此可得S阴影=${S}_{扇形AB{B}_{1}}$,根据扇形面积公式即可得出结论.
解答 解:∵${S}_{△ABC}={S}_{△A{B}_{1}{C}_{1}}$,
∴S阴影=${S}_{扇形AB{B}_{1}}$=$\frac{50}{360}$πAB2=$\frac{5}{4}$π.
故答案为:$\frac{5}{4}$π.
点评 本题考查了旋转的性质以及扇形的面积公式,解题的关键是找出S阴影=${S}_{扇形AB{B}_{1}}$.本题属于基础题,难度不大,解决该题型题目时,根据旋转的性质找出阴影部分的面积等于扇形的面积是关键.

练习册系列答案
相关题目
14.下列说法中正确的是( )
| A. | 旋转一定会改变图形的形状和大小 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| D. | 相等的角是对顶角 |
19.因式分解2x+x3的正确结果是( )
| A. | 2(x+x3) | B. | x(2+x2) | C. | 2x(1+x) | D. | x(2+x3) |
6.已知直角三角形两边的长为3和4,则第三边的长为( )
| A. | 7 | B. | 5 | C. | 5或$\sqrt{7}$ | D. | 以上都不对 |
 如图,一个机器人从点O出发,向正东方向走3米到达点A1,再向正北方向走6米到达点A2,再向正西方向走9米到达点A3,再向正南方向走12米到达点A4,再向正东方向走15米到达点A5…按此规律走下去,当机器人走到点A6时,所在的位置是(9,12)(用坐标表示)
如图,一个机器人从点O出发,向正东方向走3米到达点A1,再向正北方向走6米到达点A2,再向正西方向走9米到达点A3,再向正南方向走12米到达点A4,再向正东方向走15米到达点A5…按此规律走下去,当机器人走到点A6时,所在的位置是(9,12)(用坐标表示) 如图,在直角三角形ABC中,∠C=90°,AB=10,AC=8,点E、F分别为AC和AB的中点,则△AEF的周长等于( )
如图,在直角三角形ABC中,∠C=90°,AB=10,AC=8,点E、F分别为AC和AB的中点,则△AEF的周长等于( )