题目内容
4．把二次函数y=（x-2）2+1化为y=x2+bx+c的形式，其中b、c为常数，则b+c=1．分析 将y=（x-2）2+1化为y=x2+bx+c的形式，对应系数相等，易得b、c的值，然后求b+c的值．
解答 解：∵y=（x-2）2+1=x2-4x+5，
∴b=-4，c=5，
∴b+c=-4+5=1．
故答案是：1．
点评 本题考查了二次函数的解析式有三种形式：（1）一般式：y=ax2+bx+c（a≠0，a、b、c为常数）；（2）顶点式：y=a（x-h）2+k；（3）交点式（与x轴）：y=a（x-x1）（x-x2）．
练习册系列答案
天天练口算系列答案
相关题目
15．下列运算错误的是（ ）
| A． | x5•x5=x10 | B． | x5+x5=2x5 | ||
| C． | （-x5）5=-x25 | D． | （2x2y）3÷（$\frac{1}{4}$xy3）=$\frac{1}{2}$x5 |
19．分式方程$\frac{2}{x-3}$-$\frac{2x}{3-x}$=10的解是（ ）
| A． | 3 | B． | 2 | C． | 0 | D． | 4 |
9．
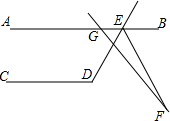如图，AB∥CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=130°，则∠F的度数是（ ）
如图，AB∥CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=130°，则∠F的度数是（ ）| A． | 10.5° | B． | 9.5° | C． | 8.5° | D． | 8° |
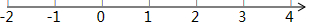
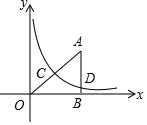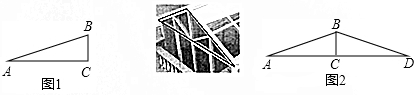
如图，AB⊥x轴，B为垂足，双曲线y=$\frac{k}{x}$（x＞0）与△AOB的两条边OA，AB分别相交于C，D两点，OC=CA，△ACD的面积为3，则k等于（ ）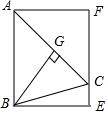
已知，△ABC中，AB=AC，∠BAC=45°，过C作CF∥AB，过A，B分别向直线CF作垂线，垂足分别为F，E，过B作BG⊥AC于G．
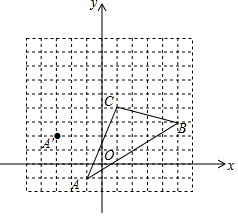如图，△ABC各顶点的坐标分别为A（-1，-1）、B（5，3）、C（1，4）．