题目内容
13.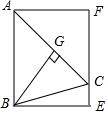 已知,△ABC中,AB=AC,∠BAC=45°,过C作CF∥AB,过A,B分别向直线CF作垂线,垂足分别为F,E,过B作BG⊥AC于G.
已知,△ABC中,AB=AC,∠BAC=45°,过C作CF∥AB,过A,B分别向直线CF作垂线,垂足分别为F,E,过B作BG⊥AC于G.(1)若AB=2$\sqrt{2}$时,求AF的长;
(2)求证:CF-CE=$\sqrt{2}$CG.
分析 (1)只要证明△ABG≌△ACF,推出推出CF=BG,只要求出BG即可解决问题.
(2)作CP∥BG交BE于P,作PH⊥BG于H,只要证明CF-CE=PB,PB=$\sqrt{2}$CG即可解决问题.
解答 (1)解:如图,∵AB∥EF,AF⊥EF,BG⊥AC,
∴∠AFC=∠AGB=∠BAF=90°,
∵∠BAC=45°,
∴∠FAC=45°,
在△ABG和△ACF中,
$\left\{\begin{array}{l}{∠BAG=∠CAF}\\{∠AGB=∠F}\\{AB=AC}\end{array}\right.$,
∴△ABG≌△ACF,
∴CF=BG,
在Rt△ABG中,AB=2$\sqrt{2}$,
∴AG=BG=2,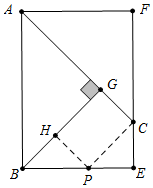
CF=2.
(2)证明:作CP∥BG交BE于P,作PH⊥BG于H,
∵∠PBH=∠HPB=45°,∠CPE=∠GBE=45°,
∴∠HPC=∠PHG=∠HGC=90°,
∴四边形HGCP是矩形,
∴GC=PH,
∵∠CPE=∠PCE=45°,
∴PE=CE,
∵AF=BE=CF,
∴CF-CE=BE-PE=PB=$\sqrt{2}$PH=$\sqrt{2}$CG,
∴CF-CE=$\sqrt{2}$CG.
点评 本题考查等腰直角三角形的性质、矩形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造特殊三角形或特殊四边形解决问题,属于中考常考题型.

练习册系列答案
相关题目
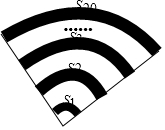 手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1,若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20=205π.
手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1,若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20=205π.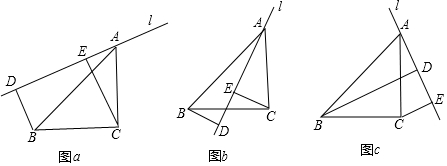
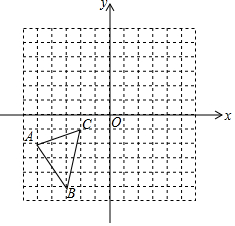 在如图的直角坐标系中,每个小方格郡是边长为1的正方形,△ABC的顶点均在格点上点A的坐标(-5,-2).
在如图的直角坐标系中,每个小方格郡是边长为1的正方形,△ABC的顶点均在格点上点A的坐标(-5,-2). 如图,点A,B,C都在⊙O上,若∠OAC=17°,∠ACB=46°,AC与OB交于点D,则∠ODA的度数为71度.
如图,点A,B,C都在⊙O上,若∠OAC=17°,∠ACB=46°,AC与OB交于点D,则∠ODA的度数为71度.