题目内容
15.已知方程x2-(k2-k-12)x+2k=0的两根互为相反数.(1)求k的值;
(2)求方程的两根.
分析 (1)根据根与系数的关系得到k2-k-12=0,然后解关于k的方程,再利用判别式的意义确定k的值;
(2)把(1)中k的值代入方程,然后利用直接开平方法解方程即可.
解答 解:(1)根据题意得k2-k-12=0,解得k1=4,k2=-3,
当k=4时,方程化为x2+8=0,△0-4×8<0,此方程没有实数解,
所以k的值为-3;
(2)当k=-3时,方程化为x2-6=0,解得x1=$\sqrt{6}$,x2=-$\sqrt{6}$.
点评 本题考查了根与系数的关系:如果x1、x2是一元二次方程ax2+bx+c=0(a≠0)的两根,那么,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
5.下列各组单项式中,不是同类项的是( )
| A. | 0.4x2y与0.3xy2 | B. | 2a2b与5ba2 | C. | 13与-$\frac{3}{2}$ | D. | -3x与7x |
6. 如图,利用标杆BE测量树CD的高度,如果标杆BE长为2米,测得AB=3米,AC=9米,且点A、E、D在一条直线上,则树CD是( )
如图,利用标杆BE测量树CD的高度,如果标杆BE长为2米,测得AB=3米,AC=9米,且点A、E、D在一条直线上,则树CD是( )
 如图,利用标杆BE测量树CD的高度,如果标杆BE长为2米,测得AB=3米,AC=9米,且点A、E、D在一条直线上,则树CD是( )
如图,利用标杆BE测量树CD的高度,如果标杆BE长为2米,测得AB=3米,AC=9米,且点A、E、D在一条直线上,则树CD是( )| A. | 6米 | B. | 7.5米 | C. | 8米 | D. | 8.5米 |
20.下列命题中,正确的是( )
| A. | 平面上三个点确定一个圆 | |
| B. | 与某圆一条半径垂直的直线是该圆的切线 | |
| C. | 三角形的外心在三角形的外面 | |
| D. | 等弧所对的圆周角相等 |
7.小婷从标有1到9序号的9张卡片中任意抽取一张,抽到序号是3的倍数的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | 1 |
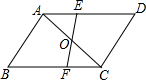 如图,在四边形ABCD中,AD∥BC,EF过AC的中点O,分别交AD,BC于点E,F.
如图,在四边形ABCD中,AD∥BC,EF过AC的中点O,分别交AD,BC于点E,F.