题目内容
19.解方程:(1)$\frac{1}{2}$x2+x-1=0(用配方法解)
(2)(2x-1)(x-1)=2x-1(用适当的方法解)
分析 (1)配方法求解可得;
(2)因式分解法求解可得.
解答 解:(1)∵x2+2x=2,
∴x2+2x+1=2+1,即(x+1)2=3,
则x+1=±$\sqrt{3}$,
∴x=-1±$\sqrt{3}$;
(2)∵(2x-1)(x-1)-(2x-1)=0,
∴(2x-1)(x-2)=0,
则2x-1=0或x-2=0,
解得:x=0.5或x=2.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
7.若点A(-1,y1),B(1,y2),C(2,y3)都在反比例函数y=$\frac{3}{x}$的图象上,则y1,y2,y3的大小关系为( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y3<y2<y1 |
8.已知一个直角三角形的两直角边长分别为3和4,则斜边长是( )
| A. | 5 | B. | $\sqrt{14}$ | C. | $\sqrt{7}$ | D. | $\sqrt{7}$或5 |
9.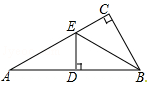 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( )
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( )
 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( )
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
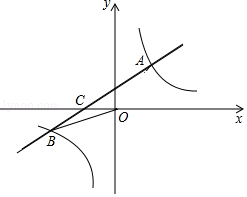 如图,在平面直角坐标系xOy中,一次函数y=ax+b(a,b是常数,且a≠0)的图象与反比例函数$y=\frac{k}{x}$(k是常数,且k≠0)的图象交于一、三象限内的A,B两点,与x轴交于点C,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{2}{5}$.
如图,在平面直角坐标系xOy中,一次函数y=ax+b(a,b是常数,且a≠0)的图象与反比例函数$y=\frac{k}{x}$(k是常数,且k≠0)的图象交于一、三象限内的A,B两点,与x轴交于点C,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{2}{5}$. 如图,根据图形填空
如图,根据图形填空