题目内容
19. 如图,在△ABC中,∠C=90°,AC=BC=a,分别以点A、B、C为圆心,a为半径$\widehat{CE}$、$\widehat{CD}$、$\widehat{AB}$,设$\widehat{CE}$与$\widehat{CD}$的长度之和为l1,$\widehat{AB}$的长为l2,则l1与l2的大小关系为( )
如图,在△ABC中,∠C=90°,AC=BC=a,分别以点A、B、C为圆心,a为半径$\widehat{CE}$、$\widehat{CD}$、$\widehat{AB}$,设$\widehat{CE}$与$\widehat{CD}$的长度之和为l1,$\widehat{AB}$的长为l2,则l1与l2的大小关系为( )| A. | l1>l2 | B. | l1=l2 | C. | l1<l2 | D. | 不能确定 |
分析 由∠C=90°,AC=BC=a知∠ABC=∠ACB=45°,再根据弧长公式求出l1、l2即可得.
解答 解:∵∠C=90°,AC=BC=a,
∴∠ABC=∠ACB=45°,
∴l1=$\frac{45•π•a}{180}$×2=$\frac{1}{2}$πa,l2=$\frac{90•π•a}{180}$=$\frac{1}{2}$πa,
∴l1=l2,
故选:B.
点评 本题主要考查等腰直角三角形和弧长公式,熟练掌握弧长公式:l=$\frac{nπR}{180}$(弧长为l,圆心角度数为n,圆的半径为R)是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.某同学骑车从学校到家,每分行1.5千米,某天回家时,速度提高到每分行2千米,结果提前5分回家,设原来从学校到家之间骑车用x分,则列方程为( )
| A. | 1.5x=2(x+5) | B. | 1.5x=2(x-5) | C. | 1.5(x+5)=2x | D. | 1.5(x-5)=2x |
 如图,在△ABc中,D是Bc边的中点,且AD=AC,DE⊥BC,DE与AB交于点E,EC与AD交于点F
如图,在△ABc中,D是Bc边的中点,且AD=AC,DE⊥BC,DE与AB交于点E,EC与AD交于点F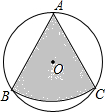 如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,求圆锥的底面圆半径(结果保留π)
如图,从一个直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,求圆锥的底面圆半径(结果保留π)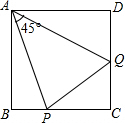 如图,在正方形ABCD中,P、Q分别为BC、CD边上的点,且∠PAQ=45°,△PCQ的周长为4,正方形ABCD的边长是多少?
如图,在正方形ABCD中,P、Q分别为BC、CD边上的点,且∠PAQ=45°,△PCQ的周长为4,正方形ABCD的边长是多少?
