题目内容
10.二元一次方程组$\left\{\begin{array}{l}x-y=3\\ 2x+y=6\end{array}\right.$的解为$\left\{\begin{array}{l}x=3\\ y=3\end{array}\right.$.分析 先用加减消元法求出x的值,再用代入消元法求出y的值即可.
解答 解:$\left\{\begin{array}{l}x-y=3①\\ 2x+y=6②\end{array}\right.$,①+②得,3x=9,解得x=3,把x=3代入①得,3-y=3,解得y=0,
故方程组的解为$\left\{\begin{array}{l}x=3\\ y=3\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}x=3\\ y=3\end{array}\right.$.
点评 本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
12.能够把三角形的面积分成相等的两部分的线段是( )
| A. | 三角形的角平分线 | B. | 三角形的高 | ||
| C. | 三角形的中线 | D. | 三角形的中位线 |
19.小华在解方程x2=-5x时,得x=-5,则他漏掉的一个根是( )
| A. | x=-5 | B. | x=0 | C. | x=-1 | D. | x=1 |
 你能把下图分成4个全等的图形吗?(画出分割线)
你能把下图分成4个全等的图形吗?(画出分割线)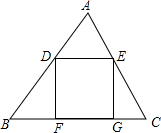 如图,在△ABC中,BC=12,AB=8$\sqrt{2}$,AC=4$\sqrt{5}$,D是AB边上的动点,DE∥BC交AC边于点E,分别过点D,E作BC边的垂线,垂足分别为,G,设AD=x.
如图,在△ABC中,BC=12,AB=8$\sqrt{2}$,AC=4$\sqrt{5}$,D是AB边上的动点,DE∥BC交AC边于点E,分别过点D,E作BC边的垂线,垂足分别为,G,设AD=x.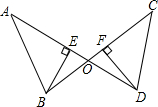 如图,AD和BC相交于点O,BE⊥AD于点E,DF⊥BC于点F,BE=DF,∠ABC=∠CDA.求证:AB=CD.
如图,AD和BC相交于点O,BE⊥AD于点E,DF⊥BC于点F,BE=DF,∠ABC=∠CDA.求证:AB=CD. 如图,在△ABC中,AB⊥EC于点E,∠ABC=45°,BD平分∠ABC且与CE交于点F,BE=a,FE=b,点M,N分别是BD,BC上的动点,当MN+MC最小时,此时动点N与点C的距离为b.
如图,在△ABC中,AB⊥EC于点E,∠ABC=45°,BD平分∠ABC且与CE交于点F,BE=a,FE=b,点M,N分别是BD,BC上的动点,当MN+MC最小时,此时动点N与点C的距离为b.