题目内容
12．
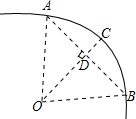如图，一条公路的转弯处是一段圆弧（图中的弧AB），点O是这段弧的圆心，C是弧AB上一点，OC⊥AB，垂足为D．若这段弯路的半径是100m，CD=20m，则A、B两点的直线距离是（ ）| A． | 60m | B． | 80m | C． | 100m | D． | 120m |
分析 先求出OD半的长，再利用勾股定理求出AD，即可得出结果．
解答 解：∵OC⊥AB，
∴AB=2AD=2BD，
∵OC=100m，CD=20m，
∴OD=80m，
根据勾股定理可得：OA2=BD2+AD2，
即1002=802+AD2，
解得：AD=60，
∴AB=2AD=120m．
故选：D．
点评 本题考查了垂径定理的应用、勾股定理；利用垂径定理和勾股定理求出线段的长是本题的关键．
练习册系列答案
相关题目
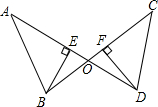如图，AD和BC相交于点O，BE⊥AD于点E，DF⊥BC于点F，BE=DF，∠ABC=∠CDA．求证：AB=CD．
如图，在△ABC中，AB⊥EC于点E，∠ABC=45°，BD平分∠ABC且与CE交于点F，BE=a，FE=b，点M，N分别是BD，BC上的动点，当MN+MC最小时，此时动点N与点C的距离为b．
2．下列各数中最小的是（ ）
| A． | -5 | B． | $\sqrt{3}$ | C． | 0 | D． | -π |