题目内容
11.如果两个相似三角形的面积比为9:16,那么这两个三角形对应边上的高之比为3:4.分析 根据相似三角形的面积的比等于相似比的平方求出相似比,根据相似三角形的性质解答即可.
解答 解:∵两个相似三角形的面积比为9:16,
∴两个相似三角形的相似比为3:4,
∴这两个三角形对应边上的高之比为3:4,
故答案为:3:4.
点评 本题考查的是相似三角形的性质,掌握相似三角形的面积的比等于相似比的平方、相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比也等于相似比是解题的关键.

练习册系列答案
相关题目
12.能够把三角形的面积分成相等的两部分的线段是( )
| A. | 三角形的角平分线 | B. | 三角形的高 | ||
| C. | 三角形的中线 | D. | 三角形的中位线 |
19.小华在解方程x2=-5x时,得x=-5,则他漏掉的一个根是( )
| A. | x=-5 | B. | x=0 | C. | x=-1 | D. | x=1 |
6.方程(x+2)2-10(x+2)+25=0的解为( )
| A. | -2 | B. | 2 | C. | -3 | D. | x1=x2=3 |
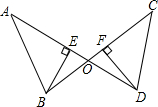 如图,AD和BC相交于点O,BE⊥AD于点E,DF⊥BC于点F,BE=DF,∠ABC=∠CDA.求证:AB=CD.
如图,AD和BC相交于点O,BE⊥AD于点E,DF⊥BC于点F,BE=DF,∠ABC=∠CDA.求证:AB=CD.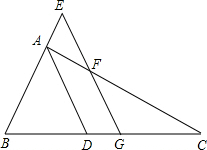 如图,AD为△ABC的角平分线,G为BC中点,GE∥AD,分别交BA的延长线于E,交AC于F,求证:
如图,AD为△ABC的角平分线,G为BC中点,GE∥AD,分别交BA的延长线于E,交AC于F,求证: 如图,在△ABC中,AB⊥EC于点E,∠ABC=45°,BD平分∠ABC且与CE交于点F,BE=a,FE=b,点M,N分别是BD,BC上的动点,当MN+MC最小时,此时动点N与点C的距离为b.
如图,在△ABC中,AB⊥EC于点E,∠ABC=45°,BD平分∠ABC且与CE交于点F,BE=a,FE=b,点M,N分别是BD,BC上的动点,当MN+MC最小时,此时动点N与点C的距离为b.