题目内容
17.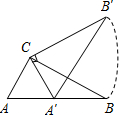 三角板ABC中,∠ACB=90°,∠B=30°,AC=2$\sqrt{3}$,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
三角板ABC中,∠ACB=90°,∠B=30°,AC=2$\sqrt{3}$,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )| A. | $\frac{3}{2}$π | B. | $\frac{4}{3}$$\sqrt{3}$π | C. | 2π | D. | 3π |
分析 首先根据勾股定理计算出BC长,再根据等边三角形的判定和性质计算出∠ACA′=60°,进而可得∠BCB′=60°,然后再根据弧长公式可得答案.
解答 解:∵∠B=30°,AC=2$\sqrt{3}$,
∴BA=4$\sqrt{3}$,∠A=60°,
∴CB=6,
∵AC=A′C,
∴∠AA′C是等边三角形,
∴∠ACA′=60°,
∴∠BCB′=60°,
∴弧长l=$\frac{nπr}{180}$=$\frac{60π×6}{180}$=2π,
故选C.
点评 此题主要考查了旋转的性质,等边三角形的判定和性质,以及弧长计算,关键是掌握弧长计算公式.

练习册系列答案
相关题目
10.在数轴上表示不等式2x>4的解集,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
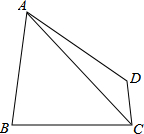 如图,在四边形ABCD中,AD=AB=BC,连接AC,且∠ACD=30°,tan∠BAC=$\frac{{2\sqrt{3}}}{3}$,CD=3,则AC=6$\sqrt{3}$.
如图,在四边形ABCD中,AD=AB=BC,连接AC,且∠ACD=30°,tan∠BAC=$\frac{{2\sqrt{3}}}{3}$,CD=3,则AC=6$\sqrt{3}$.