题目内容
2.如图1,点D为△ABC边BC的延长线上一点.(1)若∠A:∠ABC=3:4,∠ACD=140°,求∠A的度数;
(2)若∠ABC的角平分线与∠ACD的角平分线交于点M,过点C作CP⊥BM于点P.求证:∠MCP=90°-$\frac{1}{2}$∠A;
(3)在(2)的条件下,将△MBC以直线BC为对称轴翻折得到△NBC,∠NBC的角平分线与∠NCB的角平分线交于点Q(如图2),试探究∠BQC与∠A有怎样的数量关系,请写出你的猜想并证明.
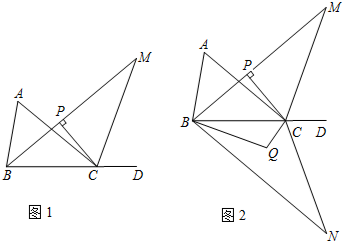
分析 (1)先根据∠A:∠ABC=3:4,设∠A=3k,∠ABC=4k,再由三角形外角的性质求出k的值,进而可得出结论;
(2)根据三角形外角的性质得出∠M=∠MCD-∠MBC,∠A=∠ACD-∠ABC.再由MC、MB分别平分∠ACD、∠ABC得出∠MCD=$\frac{1}{2}$∠ACD,∠MBC=$\frac{1}{2}$∠ABC,故∠M=$\frac{1}{2}$(∠ACD-∠ABC)=$\frac{1}{2}$∠A.根据CP⊥BM即可得出结论;
(3)根据BQ平分∠CBN,CQ平分∠BCN可知∠QBC=$\frac{1}{2}$∠CBN,∠QCB=$\frac{1}{2}$∠BCN,再根据三角形内角和定理可知,∠Q=180°-$\frac{1}{2}$(∠CBN+∠BCN)=$\frac{1}{2}$(180°-∠N)=90°+$\frac{1}{2}$∠N.由(2)知:∠M=$\frac{1}{2}$∠A.根据轴对称性质知:∠M=∠N,由此可得出结论.
解答 (1)解:∵∠A:∠ABC=3:4,
∴可设∠A=3k,∠ABC=4k,
又∵∠ACD=∠A+∠ABC=140°,
∴3k+4k=140°,
解得k=20°.
∴∠A=3k=60°.
(2)证明:∵∠MCD是△MBC的外角,
∴∠M=∠MCD-∠MBC.
同理可得,∠A=∠ACD-∠ABC.
∵MC、MB分别平分∠ACD、∠ABC,
∴∠MCD=$\frac{1}{2}$∠ACD,∠MBC=$\frac{1}{2}$∠ABC,
∴∠M=$\frac{1}{2}$(∠ACD-∠ABC)=$\frac{1}{2}$∠A.
∵CP⊥BM,
∴∠PCM=90°-∠M=90°-$\frac{1}{2}$∠A.
(3)猜想∠BQC=90°+$\frac{1}{4}$∠A.
证明如下:
∵BQ平分∠CBN,CQ平分∠BCN,
∴∠QBC=$\frac{1}{2}$∠CBN,∠QCB=$\frac{1}{2}$∠BCN,
∴∠Q=180°-$\frac{1}{2}$(∠CBN+∠BCN)=$\frac{1}{2}$(180°-∠N)=90°+$\frac{1}{2}$∠N.
由(2)知:∠M=$\frac{1}{2}$∠A.
又由轴对称性质知:∠M=∠N,
∴∠BQC=90°+$\frac{1}{4}$∠A.
点评 本题考查的是三角形内角和定理,在解答此题时要注意轴对称的性质及翻折变换、三角形外角的性质及角平分线的性质等知识的灵活运用,难度适中.

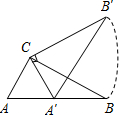 三角板ABC中,∠ACB=90°,∠B=30°,AC=2$\sqrt{3}$,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
三角板ABC中,∠ACB=90°,∠B=30°,AC=2$\sqrt{3}$,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )| A. | $\frac{3}{2}$π | B. | $\frac{4}{3}$$\sqrt{3}$π | C. | 2π | D. | 3π |
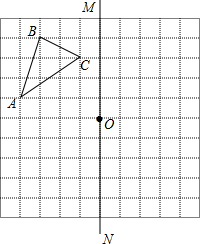 如图,每个小方格都是边长为1个单位长度的小正方形.
如图,每个小方格都是边长为1个单位长度的小正方形. △ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,作出△ABC关于原点O对称的△A1B1C1,并写出点C1的坐标.
△ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,作出△ABC关于原点O对称的△A1B1C1,并写出点C1的坐标.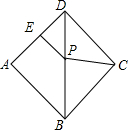 如图,在菱形ABCD中,∠ADC=70°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB=70度.
如图,在菱形ABCD中,∠ADC=70°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB=70度.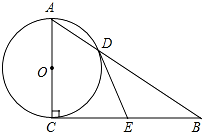 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线DE,交BC于E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线DE,交BC于E.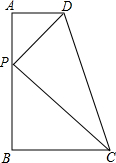 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=3,CD=5$\sqrt{2}$,点P在线段AB上.若△PCD是以点P为直角顶点的直角三角形,则AP=1或6.
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=3,CD=5$\sqrt{2}$,点P在线段AB上.若△PCD是以点P为直角顶点的直角三角形,则AP=1或6.