题目内容
6．若$\frac{1}{3}$x2m-1y2n与3x3y是同类项，则m=2，n=$\frac{1}{2}$．分析 利用同类项的定义求解即可．
解答 解：∵$\frac{1}{3}$x2m-1y2n与3x3y是同类项，
∴2m-1=3，2n=1，解得m=2，m=$\frac{1}{2}$．
故答案为：2，$\frac{1}{2}$．
点评 本题主要考查同类项，解题的关键是熟记同类项的定义．
练习册系列答案
相关题目
17．
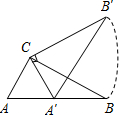三角板ABC中，∠ACB=90°，∠B=30°，AC=2$\sqrt{3}$，三角板绕直角顶点C逆时针旋转，当点A的对应点A′落在AB边的起始位置上时即停止转动，则B点转过的路径长为（ ）
三角板ABC中，∠ACB=90°，∠B=30°，AC=2$\sqrt{3}$，三角板绕直角顶点C逆时针旋转，当点A的对应点A′落在AB边的起始位置上时即停止转动，则B点转过的路径长为（ ）| A． | $\frac{3}{2}$π | B． | $\frac{4}{3}$$\sqrt{3}$π | C． | 2π | D． | 3π |
15．已知$\sqrt{a-1}$+$\sqrt{1-a}$有意义，且|b-3|+$\sqrt{c-2}$+（d-2015）2=0，求（$\sqrt{2}$）-a+（$\sqrt{2}$）b+（$\frac{1}{\sqrt{2}-1}$）c+（-1）d=（ ）
| A． | 4$\sqrt{2}$+2 | B． | 3 | C． | $\frac{9}{2}$$\sqrt{2}$+2 | D． | 3+2$\sqrt{2}$ |
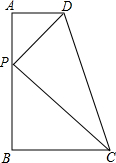如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=2，BC=3，CD=5$\sqrt{2}$，点P在线段AB上．若△PCD是以点P为直角顶点的直角三角形，则AP=1或6．