题目内容
9.已知点A(3x-2y,y+1)在象限的角平分线上,且点A的横坐标为5,求x、y的值.分析 根据象限的角平分线上点的坐标特征分类讨论:当点A(3x-2y,y+1)在第一、三象限的角平分线上,则3x-2y=5,3x-2y=y+1;当点A(3x-2y,y+1)在第二、四象限的角平分线上,则3x-2y=5,3x-2y+y+1=0,然后分别解方程组求出对应的x和y的值.
解答 解:当点A(3x-2y,y+1)在第一、三象限的角平分线上,则3x-2y=5,3x-2y=y+1,解得x=$\frac{13}{3}$,y=4;
当点A(3x-2y,y+1)在第二、四象限的角平分线上,则3x-2y=5,3x-2y+y+1=0,解得x=-$\frac{7}{3}$,y=-6,
所以x、y的值分别为$\frac{13}{3}$,y=4或-$\frac{7}{3}$,y=-6.
点评 本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系.

练习册系列答案
相关题目
17.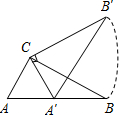 三角板ABC中,∠ACB=90°,∠B=30°,AC=2$\sqrt{3}$,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
三角板ABC中,∠ACB=90°,∠B=30°,AC=2$\sqrt{3}$,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
 三角板ABC中,∠ACB=90°,∠B=30°,AC=2$\sqrt{3}$,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
三角板ABC中,∠ACB=90°,∠B=30°,AC=2$\sqrt{3}$,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )| A. | $\frac{3}{2}$π | B. | $\frac{4}{3}$$\sqrt{3}$π | C. | 2π | D. | 3π |
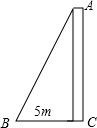 如图,小明想知道学校旗杆的高度,他把升旗绳子一端挂在旗杆顶端,发现绳子垂到地面时还余1m;当他把绳子下端拉开5m后,绳子下端刚好接触到地面,则旗杆高度为12m.
如图,小明想知道学校旗杆的高度,他把升旗绳子一端挂在旗杆顶端,发现绳子垂到地面时还余1m;当他把绳子下端拉开5m后,绳子下端刚好接触到地面,则旗杆高度为12m. 已知:DE∥BC,求证:DG•BF=GE•FC.
已知:DE∥BC,求证:DG•BF=GE•FC. 如图,已知∠AOB=60°,点P在边OA上,OP=20,点M,N在边OB上,PM=PN.若MN=6,则OM=( )
如图,已知∠AOB=60°,点P在边OA上,OP=20,点M,N在边OB上,PM=PN.若MN=6,则OM=( )