Question

11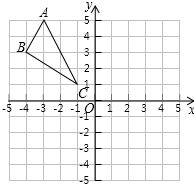．如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（-3，5）、B（-4，3）、C（-1，1）
（1）作出△ABC关于直线x=1对称的△A₁B₁C₁；
（2）B₁点的坐标（6，3），C₁点的坐标（3，1）；
（3）C点与C₂点关于直线x=n对称，则C₂的坐标（2n+1，1）（用含有n的式子表示）

Answer 1

分析 （1）利用已知坐标系结合△ABC关于直线x=1对称得出各点坐标进而得出答案；
（2）利用所画图形，进而得出对应点坐标；
（3）利用关于x=n对称点的坐标性质，设C₂的横坐标为x，则$\frac{-1+x}{2}$=n，进而得出答案．

解答 解：（1）如图：

（2）B₁点的坐标为：（6，3），C₁点的坐标为：（3，1）；
故答案为：（6，3），（3，1）；

（3）∵C点与C₂点关于直线x=n对称，
∴设C₂的坐标为：（x，1），
则$\frac{-1+x}{2}$=n，
解得：x=2n+1，
则C₂的坐标为：（2n+1，1）．
故答案为：（2n+1，1）．

点评 此题主要考查了轴对称变换，正确把握轴对称图形的性质得出对应点关系是解题关键．