题目内容
19. 如图,在△ABC中,∠C=90°,AC=8,BC=6,DE是△ABD的边AB上的高,且AD=$2\sqrt{5}$,BD=$4\sqrt{5}$.求:DE的长.
如图,在△ABC中,∠C=90°,AC=8,BC=6,DE是△ABD的边AB上的高,且AD=$2\sqrt{5}$,BD=$4\sqrt{5}$.求:DE的长.
分析 先根据勾股定理求出AB,再根据勾股定理的逆定理求出△ABD是直角三角形,然后由三角形的面积即可求出DE的长.
解答 解:∵∠C=90°,AC=8,BC=6,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∵AD2+BD2=(2$\sqrt{5}$)2+(4$\sqrt{5}$)2=100=AB2,
∴△ABD是直角三角形,∠ADB=90°,
∴△ABD的面积=$\frac{1}{2}$AB•DE=$\frac{1}{2}$AD•BD,
∴DE=$\frac{AD•BD}{AB}$=$\frac{2\sqrt{5}×4\sqrt{5}}{10}$=4.
点评 本题考查了三角形面积、勾股定理的逆定理、勾股定理;熟练掌握勾股定理,由勾股定理的逆定理证出△ABD是直角三角形是解决问题的关键.

练习册系列答案
相关题目
10.下列说法正确的是( )
| A. | 中位数就是一组数据中最中间的一个数 | |
| B. | 如果x1,x2,x3…xn的平均数是$\overline x$,那么$({{x_1}-\overline x})+({{x_2}-\overline x})+…+({{x_n}-\overline x})=0$ | |
| C. | 8,9,9,10,10,11这组数据的众数是9 | |
| D. | 一组数据的方差是这组数据的极差的平方 |
7.某青年排球队10名队员年龄情况如下:20,20,18,19,19,19,21,21,22,22,则这10名队员年龄的众数、中位数分别是( )
| A. | 20,19 | B. | 19,19 | C. | 19,20.5 | D. | 19,20 |
14.在下列各数中是无理数的有( )
-0.333…,$\sqrt{4}$,$\sqrt{5}$,$\root{3}{-8}$,-π,2.010,4.0123456…(小数部分由相继的正整数组成).
-0.333…,$\sqrt{4}$,$\sqrt{5}$,$\root{3}{-8}$,-π,2.010,4.0123456…(小数部分由相继的正整数组成).
| A. | 1个 | B. | 3个 | C. | 4个 | D. | 5个 |
8.cos60°-sin30°+tan45°的值为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
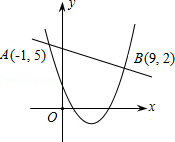 如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,5)、B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为-1≤x≤9.
如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,5)、B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为-1≤x≤9.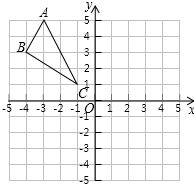 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,5)、B(-4,3)、C(-1,1)
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,5)、B(-4,3)、C(-1,1)