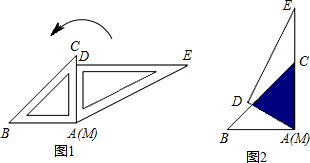题目内容
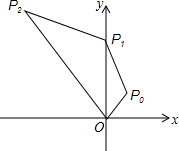 如图,在直角坐标系中,点P0的坐标为(
如图,在直角坐标系中,点P0的坐标为(
| ||
| 2 |
| ||
| 2 |
考点:规律型:点的坐标
专题:
分析:根据题意得出OP0=1,OP1=2,OP2=4,如此下去,得到线段OP3=8=23,OP4=16=24…,OPn=2n,再利用旋转角度得出点P2014的坐标与点P6的坐标在同一直线上,进而得出答案.
解答:解:∵点P0的坐标为(
,
),将线段OP0绕点O按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;
∴OP0=1,OP1=2,
∴OP2=4,如此下去,得到线段OP3=8=23,OP4=16=24…,
∴OPn=2n,
由题意可得出线段每旋转8次旋转一周,
∵2014÷8=251…6,
∴点P2014的坐标与点P6的坐标在同一直线上,正好在y轴的负半轴上,
∴点P2014的坐标是(0,-22014).
故答案为:(0,-22014).
| ||
| 2 |
| ||
| 2 |
∴OP0=1,OP1=2,
∴OP2=4,如此下去,得到线段OP3=8=23,OP4=16=24…,
∴OPn=2n,
由题意可得出线段每旋转8次旋转一周,
∵2014÷8=251…6,
∴点P2014的坐标与点P6的坐标在同一直线上,正好在y轴的负半轴上,
∴点P2014的坐标是(0,-22014).
故答案为:(0,-22014).
点评:此题主要考查了点的变化规律,根据题意得出点P2014的坐标与点P6的坐标在同一直线上是解题关键.

练习册系列答案
相关题目
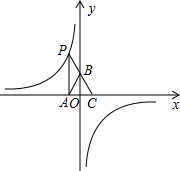 如图,点P是反比例函数y=
如图,点P是反比例函数y=| k |
| x |
| 5 |
| A、0<a<2 | ||||||||
B、
| ||||||||
C、0<a<2或a<
| ||||||||
D、0<a<2或
|
一组数据的方差为9,将这组数据中的每个数据扩大3倍,得到一组新数据的方差是( )
| A、9 | B、27 | C、81 | D、243 |
在Rt△ABC中,∠ACB=90°,∠A=30°,AC=
cm,则AB边上的中线长为( )
| 3 |
| A、1cm | ||
| B、1.5cm | ||
| C、2cm | ||
D、
|
 如图,若“车”位于点(-5,-2),“将”位于点(-1,-2),则“马”位于
如图,若“车”位于点(-5,-2),“将”位于点(-1,-2),则“马”位于