题目内容
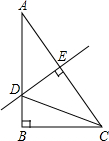 如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交于D,E为垂足,连接CD,若BD=1,求AC的长.
如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交于D,E为垂足,连接CD,若BD=1,求AC的长.考点:线段垂直平分线的性质,含30度角的直角三角形
专题:几何图形问题,数形结合
分析:由DE垂直平分斜边AC,可得AD=CD,又由在Rt△ABC中,∠A=30°,即可求得∠BCD的度数,继而求得AB的长,则可求得答案.
解答:解:∵DE垂直平分斜边AC,
∴AD=CD,
∴∠ACD=∠A=30°,
∵在Rt△ABC中,∠A=30°,
∴∠ACB=90°-∠A=60°,
∴∠BCD=∠ACB-∠ACD=30°,
∵在Rt△BCD中,BD=1,
∴CD=2BD=2,
∴AD=CD=2,
∴AB=AD+BD=3,
∴AC=
=2
.
∴AD=CD,
∴∠ACD=∠A=30°,
∵在Rt△ABC中,∠A=30°,
∴∠ACB=90°-∠A=60°,
∴∠BCD=∠ACB-∠ACD=30°,
∵在Rt△BCD中,BD=1,
∴CD=2BD=2,
∴AD=CD=2,
∴AB=AD+BD=3,
∴AC=
| AB |
| cos30° |
| 3 |
点评:此题考查了线段垂直平分线的性质以及含30°角的直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 如图所示,已知∠1=65°,∠2=115°,∠3=115°,请用两种不同方法说明AB∥CD.
如图所示,已知∠1=65°,∠2=115°,∠3=115°,请用两种不同方法说明AB∥CD. 如图所示,王师傅将两块相同的长方形木板AB,CD平行放置间隔一定距离,再用长、宽相等的两块铁片a,b分别搭在AB,CD上,再用螺丝固定,做成了一个简易的冰箱底垫.已知∠l=90°,用量角器度量出哪一个角,就可以判断铁片a与b是否为平行关系呢?
如图所示,王师傅将两块相同的长方形木板AB,CD平行放置间隔一定距离,再用长、宽相等的两块铁片a,b分别搭在AB,CD上,再用螺丝固定,做成了一个简易的冰箱底垫.已知∠l=90°,用量角器度量出哪一个角,就可以判断铁片a与b是否为平行关系呢?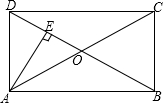 如图所示,已知矩形ABCD的对角线AC与BD相交于点0,AE丄BD于点E,且DE=OE,则∠OAB=
如图所示,已知矩形ABCD的对角线AC与BD相交于点0,AE丄BD于点E,且DE=OE,则∠OAB=