题目内容
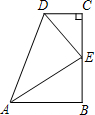 如图,∠B=∠C=90°,E是BC的中点,DE平分线∠ADC,则下列结论不正确是( )
如图,∠B=∠C=90°,E是BC的中点,DE平分线∠ADC,则下列结论不正确是( )| A、AE平分∠DAE |
| B、AB∥CD |
| C、△EBA≌△DCE |
| D、AB+CD=AD |
考点:全等三角形的判定与性质,平行线的判定
专题:
分析:由∠B=∠C=90°,直接得出选项B成立;作EF⊥AD垂足为点F,证得△DEF≌△DCE和△AFE≌△ABE,得出选项A、选项D成立;因为AB≠CD,AE≠DE,不可能得出选项C成立;由此得出结论即可.
解答: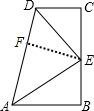 解:∵∠B=∠C=90°,
解:∵∠B=∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故B正确;
如图,作EF⊥AD垂足为点F,
∴∠DFE=90°,
∴∠DFE=∠C,
∵DE平分∠ADC,
∴∠FDE=∠CDE,
在△DEF和△DCE中;
,
∴△DEF≌△DCE(AAS);
∴CE=EF,DC=DF,∠CED=∠FED,
又∵∠B=∠C=∠DFE=90°,AE=AE,
在Rt△AFE和Rt△ABE中,
,
∴Rt△AFE≌Rt△ABE(HL);
∴AF=AB,∠FAE=∠BAE,∠AEF=∠AEB,
∴AE平分∠DAB,故A正确;
AD=AF+DF=AB+CD,故D正确;
∠AED=∠FED+AEF=
∠FEC+
∠BEF=90°,即AE⊥DE.
∵AB≠CD,AE≠DE,
∴△EBA≌△DCE不可能成立.即C不正确;
故选:C.
 解:∵∠B=∠C=90°,
解:∵∠B=∠C=90°,∴∠B+∠C=180°,
∴AB∥CD,故B正确;
如图,作EF⊥AD垂足为点F,
∴∠DFE=90°,
∴∠DFE=∠C,
∵DE平分∠ADC,
∴∠FDE=∠CDE,
在△DEF和△DCE中;
|
∴△DEF≌△DCE(AAS);
∴CE=EF,DC=DF,∠CED=∠FED,
又∵∠B=∠C=∠DFE=90°,AE=AE,
在Rt△AFE和Rt△ABE中,
|
∴Rt△AFE≌Rt△ABE(HL);
∴AF=AB,∠FAE=∠BAE,∠AEF=∠AEB,
∴AE平分∠DAB,故A正确;
AD=AF+DF=AB+CD,故D正确;
∠AED=∠FED+AEF=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB≠CD,AE≠DE,
∴△EBA≌△DCE不可能成立.即C不正确;
故选:C.
点评:本题题综合考查了角平分线的性质、三角形全等的判定与性质等知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
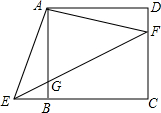 如图,在正方形ABCD中,F是CD上的一点,AE⊥AF,E是BC的延长线上一点,EF交AB于点G.
如图,在正方形ABCD中,F是CD上的一点,AE⊥AF,E是BC的延长线上一点,EF交AB于点G. 如图,△ABC和△DEF关于某点对称
如图,△ABC和△DEF关于某点对称 如图所示,点C是线段AB上的一点,点M是线段AC的中点,点N是线段BC的中点.
如图所示,点C是线段AB上的一点,点M是线段AC的中点,点N是线段BC的中点. 如图,D、E分别是△ABC的边AC、AB上的点.AE=1.5,AC=2,BC=3,且
如图,D、E分别是△ABC的边AC、AB上的点.AE=1.5,AC=2,BC=3,且 如图,在正八边形ABCDEFGH中,AC、GC是两条对角线,则∠ACG=
如图,在正八边形ABCDEFGH中,AC、GC是两条对角线,则∠ACG=