题目内容
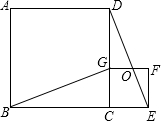 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③| DG |
| GC |
| GO |
| CE |
| A、①②③ | B、②③④ |
| C、①②④ | D、①②③④ |
考点:相似三角形的判定与性质,全等三角形的判定与性质,正方形的性质
专题:
分析:①由正方形的性质可证得△BCG≌△DCE;②结合①的结论可得∠GBC+∠DEC=90°,可得BG⊥DE;③由GO∥CE可得
=
;④由DG∥EF可得△DGO∽△EFO,可得相似比,进一步可求得面积比,找到面积之间的关系.
| DG |
| DC |
| GO |
| CE |
解答:解:∵四边形ABCD、CEFG都是正方形,
∴∠BCG=∠DCE=90°,BC=CD,GC=CE,
在△BCG和△DCE中,
,
∴△BCG≌△DCE(SAS),
∴①正确;
如图,延长BG交DE于点H,

由①可得到∠GBC=∠EDC,且∠EDC+∠CED=90°,
∴∠GBC+∠CED=90°,
∴∠BHE=90°,
∴BG⊥DE,
∴②正确;
∵GF∥CE,
∴
=
,
∴③不正确;
∵DG∥EF,
∴△DGO∽△EFO,且DG=DC-CG=a-b,EF=b
∴
=(
)2=
,
∴(a-b)2•S△EFO=b2S△DGO,
∴④正确;
综上可知正确的为①②④,
故选C.
∴∠BCG=∠DCE=90°,BC=CD,GC=CE,
在△BCG和△DCE中,
|
∴△BCG≌△DCE(SAS),
∴①正确;
如图,延长BG交DE于点H,

由①可得到∠GBC=∠EDC,且∠EDC+∠CED=90°,
∴∠GBC+∠CED=90°,
∴∠BHE=90°,
∴BG⊥DE,
∴②正确;
∵GF∥CE,
∴
| DG |
| DC |
| GO |
| CE |
∴③不正确;
∵DG∥EF,
∴△DGO∽△EFO,且DG=DC-CG=a-b,EF=b
∴
| S△DGO |
| S△EFO |
| DG |
| EF |
| (a-b)2 |
| b2 |
∴(a-b)2•S△EFO=b2S△DGO,
∴④正确;
综上可知正确的为①②④,
故选C.
点评:本题主要考查正方形的性质、全等三角形的判定和性质及相似三角形的判定和性质,综合性较强,掌握三角形全等、相似的判定和性质是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若函数y=
与y=kx的图象的一个交点为(-2,3),则它们图象的另一个交点为( )
| k |
| x |
| A、(-3,2) |
| B、(2,-3) |
| C、(-2,-3) |
| D、(-3,-2) |
 如图所示,点C是线段AB上的一点,点M是线段AC的中点,点N是线段BC的中点.
如图所示,点C是线段AB上的一点,点M是线段AC的中点,点N是线段BC的中点. 如图,在正八边形ABCDEFGH中,AC、GC是两条对角线,则∠ACG=
如图,在正八边形ABCDEFGH中,AC、GC是两条对角线,则∠ACG= 如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于点E、D,若AC=3,BC=5,则DE的长为( )
如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于点E、D,若AC=3,BC=5,则DE的长为( ) 如图,按下列要求作图:
如图,按下列要求作图: