题目内容
5.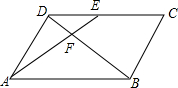 如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,DE:EC=1:2,FB=12,则DF=( )
如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,DE:EC=1:2,FB=12,则DF=( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
分析 根据平行四边形的性质易证△DEF∽△BAF,再根据相似三角形的性质:对应边的比值相等即可得到答案.
解答 解:
∵四边形ABCD是平行四边形,
∴DC∥AB,CD=AB.
∴△DEF∽△BFA,
∴DE:AB=DF:BF,
∵DE:EC=1:2,
∴DE:DC=DE:AB=1:3,
∵FB=12,
∴DF:12=1:3,
∴DF=4,
故选C.
点评 本题考查的是相似三角形的判定与性质及平行四边形的性质,熟知相似三角形各种判断方法和性质是解答此题的关键.

练习册系列答案
相关题目
10.某单位招聘,总成绩由笔试的70%和面试的30%两部分组成.已知甲应聘者笔试x分,面试y分,乙应聘者笔试y分,面试x分,而他们的总成绩相差4分,则|x-y|的值为( )
| A. | 8 | B. | 10 | C. | 12 | D. | 16 |
14.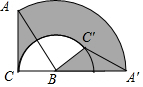 如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
 如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )| A. | 4π+2$\sqrt{3}$ | B. | $\frac{16}{3}$π-2$\sqrt{3}$ | C. | $\frac{16}{3}$π+2$\sqrt{3}$ | D. | 4π |
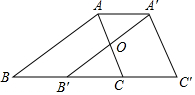 如图,在△ABC中,BC=6,将△ABC沿BC方向平移得到△A′B′C′,连接AA′,若A′B′恰好经过AC的中点O,则AA′的长度为3.
如图,在△ABC中,BC=6,将△ABC沿BC方向平移得到△A′B′C′,连接AA′,若A′B′恰好经过AC的中点O,则AA′的长度为3. 如图,E、F分别为正方形ABCD的边AB、AD上的点,且AE=AF,连接EF,将△AEF绕点A逆时针旋转45°,使E落在E1,F落在F1,连接BE1并延长交DF1于点G,如果AB=2$\sqrt{2}$,AE=1,则DG=$\frac{4\sqrt{5}}{5}$.
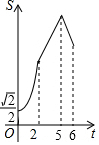
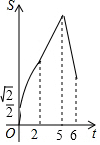
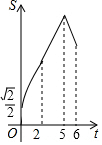
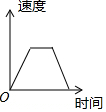
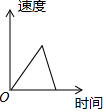
如图,E、F分别为正方形ABCD的边AB、AD上的点,且AE=AF,连接EF,将△AEF绕点A逆时针旋转45°,使E落在E1,F落在F1,连接BE1并延长交DF1于点G,如果AB=2$\sqrt{2}$,AE=1,则DG=$\frac{4\sqrt{5}}{5}$.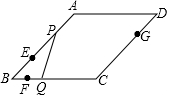 如图,在菱形ABCD中,∠ABC=45°,AB=6,点E、F、G分别是AB、BC、DC上的点,其中BE=DG=2,BF=1.点P从E点出发,以每秒2个单位长度沿折线EA-AD-DG运动;点Q以每秒1个单位沿折线FC-CG运动,当其中一个点到达后,另一个点也停止运动,设△BPQ的面积为S,点P,Q的运动时间为t秒,则S与t的函数关系的大致图象是( )
如图,在菱形ABCD中,∠ABC=45°,AB=6,点E、F、G分别是AB、BC、DC上的点,其中BE=DG=2,BF=1.点P从E点出发,以每秒2个单位长度沿折线EA-AD-DG运动;点Q以每秒1个单位沿折线FC-CG运动,当其中一个点到达后,另一个点也停止运动,设△BPQ的面积为S,点P,Q的运动时间为t秒,则S与t的函数关系的大致图象是( )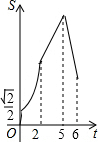
 如图,C是线段AB的中点.
如图,C是线段AB的中点.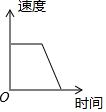
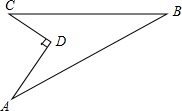 我校要对如图所示的一块地进行绿化,已知AD=4米,CD=3米,AD⊥DC,AB=13米,BC=12米,求这块地的面积.
我校要对如图所示的一块地进行绿化,已知AD=4米,CD=3米,AD⊥DC,AB=13米,BC=12米,求这块地的面积.