题目内容
14.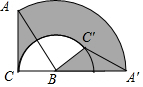 如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )| A. | 4π+2$\sqrt{3}$ | B. | $\frac{16}{3}$π-2$\sqrt{3}$ | C. | $\frac{16}{3}$π+2$\sqrt{3}$ | D. | 4π |
分析 根据扇形面积公式S=$\frac{nπ{R}^{2}}{360}$求出扇形ABA′的面积和扇形CBC′的面积,根据图形可得图中阴影部分的面积=Rt△ABC+扇形ABA′的面积-扇形CBC′的面积计算即可.
解答 解:∵AB=4,∠A=30°,
∴BC=2,AC=2$\sqrt{3}$,
∴图中阴影部分的面积
=Rt△ABC+扇形ABA′的面积-扇形CBC′的面积
=2$\sqrt{3}$×2÷2+$\frac{120×π×{4}^{2}}{360}$-$\frac{120×π×{2}^{2}}{360}$
=2$\sqrt{3}$+$\frac{16}{3}$π-$\frac{4}{3}$π
=4π+2$\sqrt{3}$.
故选:A.
点评 本题考查的是轨迹、扇形面积的计算和旋转的性质,掌握扇形面积公式S=$\frac{nπ{R}^{2}}{360}$是解题的关键.

练习册系列答案
相关题目
8.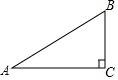 如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
 如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{7}}{4}$ | D. | $\frac{4}{5}$ |
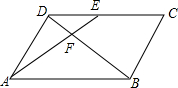 如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,DE:EC=1:2,FB=12,则DF=( )
如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,DE:EC=1:2,FB=12,则DF=( ) 如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO,并延长AO交⊙O于点E,与PB的延长线交于点D.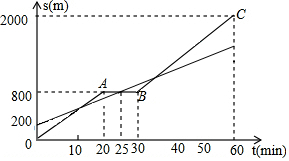 小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象. 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF
如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF 如图,在平面直角坐标系xOy中,二次函数y=x2-2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.
如图,在平面直角坐标系xOy中,二次函数y=x2-2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.