题目内容
10.学校决定购买A、B两种型号电脑,若购买A型电脑3台,B型电脑8台共需40000元;若购买A型电脑14台,B型电脑4台共需80000元.(1)A、B两种型号电脑每台多少元?
(2)若用不超过160000元去购买A、B两种型号电脑共45台,则最多可购买A型电脑多少台?
分析 (1)设A型电脑x元/台,B型电脑y元/台.然后根据购买A型电脑3台,B型电脑8台共需40000元;若购买A型电脑14台,B型电脑4台共需80000元列方程组求解即可;
(2)设购买a台A型电脑,(45-a)台B型电脑.然后根据总费用不超过160000元列不等式求解即可.
解答 解:(1)设A型电脑x元/台,B型电脑y元/台.
根据题意得:$\left\{\begin{array}{l}{3x+8y=40000}\\{14x+4y=80000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4800}\\{y=3200}\end{array}\right.$
答:A型电脑4800元/台,B型电脑3200元/台.
(2)设购买a台A型电脑,(45-a)台B型电脑.
根据题意得:4800a+3200(45-a)≤160000,
解得:a≤10
答:最多购买10台A型电脑.
点评 本题主要考查的是一元一次不等式的应用和二元一次方程的应用,根据题意列出方程组和不等式是解题的关键.

练习册系列答案
相关题目
15.下列方程的变形中,正确的是( )
| A. | 由$-\frac{1}{3}$x=0,得x=3 | B. | 由6y=3,得y=2 | ||
| C. | 由x-5=-3,得x=5+3 | D. | 由2=x-4,得x=4+2 |
19. 如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E,AE=2,CE=( )
如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E,AE=2,CE=( )
 如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E,AE=2,CE=( )
如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E,AE=2,CE=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |

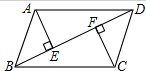 如图,BD是?ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:AE=CF.
如图,BD是?ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:AE=CF. 如图,点P为△ABC三边垂直平分线的交点,若∠PAC=20°,∠PCB=30°,求∠PAB的度数.
如图,点P为△ABC三边垂直平分线的交点,若∠PAC=20°,∠PCB=30°,求∠PAB的度数.