题目内容
20. 如图,点P为△ABC三边垂直平分线的交点,若∠PAC=20°,∠PCB=30°,求∠PAB的度数.
如图,点P为△ABC三边垂直平分线的交点,若∠PAC=20°,∠PCB=30°,求∠PAB的度数.
分析 由P为△ABC三边垂直平分线的交点,推出PA=PC=PB,由等腰三角形的性质证得∠PAC=∠PCA=20°,∠PBC=∠PCN=30°,由∠PAB=∠PBA,根据三角形的内角和即可推出结论.
解答 解:∵P为△ABC三边垂直平分线的交点,
∴PA=PC=PB,
∴∠PAC=∠PCA=20°,
∠PBC=∠PCN=30°,
∵∠PAB=∠PBA,
∴∠PAB=$\frac{1}{2}$(180°-2×20°-2×30°)=40°.
点评 本题主要考查线段垂直平分线的性质,等腰三角形的性质,利用线段垂直平分线的性质得到PA=PB=PC是解题的关键.

练习册系列答案
相关题目
15.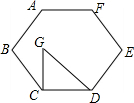 如图,正六边形ABCDEF的边CD与等腰三角形GCD的直角边CD重合,∠GCD=90°,点G在正六边形的内部,则∠EDG的度数为( )
如图,正六边形ABCDEF的边CD与等腰三角形GCD的直角边CD重合,∠GCD=90°,点G在正六边形的内部,则∠EDG的度数为( )
 如图,正六边形ABCDEF的边CD与等腰三角形GCD的直角边CD重合,∠GCD=90°,点G在正六边形的内部,则∠EDG的度数为( )
如图,正六边形ABCDEF的边CD与等腰三角形GCD的直角边CD重合,∠GCD=90°,点G在正六边形的内部,则∠EDG的度数为( )| A. | 90° | B. | 85° | C. | 65° | D. | 75° |
10.等腰三角形的顶角为100°,则它的一个底角是( )
| A. | 40° | B. | 50° | C. | 60° | D. | 80° |
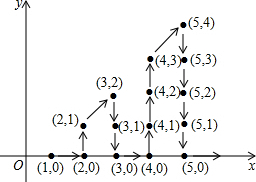 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)根据这个规律探索可得,第2016个点的横坐标为63.
如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)根据这个规律探索可得,第2016个点的横坐标为63.