题目内容
14．正比例函数y=（2k-3）x的图象过点（3，-9），则k的值为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 根据一次函数图象上点的坐标特征即可得出关于k的一元一次方程，解之即可得出结论．
解答 解：∵正比例函数y=（2k-3）x的图象过点（3，-9），
∴-9=3（2k-3），
解得：k=0．
故选A．
点评 本题考查了一次函数图象上点的坐标特征，根据一次函数图象上点的坐标特征找出关于k的一元一次方程是解题的关键．
练习册系列答案
相关题目
4．下列四个图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
5．
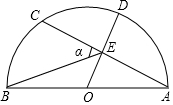如图，AB是半圆的直径，点O为圆心，OA=5，弦AC=8，OD⊥AC，垂足为E，交⊙O于D，连接BE，设∠BEC=α，则tanα的值为（ ）
如图，AB是半圆的直径，点O为圆心，OA=5，弦AC=8，OD⊥AC，垂足为E，交⊙O于D，连接BE，设∠BEC=α，则tanα的值为（ ）| A． | $\frac{3}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{5}{4}$ | D． | $\frac{2}{3}$ |
2．
如图，⊙O是△ABC的内切圆，D，E是切点，∠A=50°，∠C=60°，则∠DOE的度数为（ ）
如图，⊙O是△ABC的内切圆，D，E是切点，∠A=50°，∠C=60°，则∠DOE的度数为（ ）| A． | 70° | B． | 110° | C． | 120° | D． | 130° |
9．比较-2，-$\frac{1}{2}$，0，0.02的大小，正确的是（ ）
| A． | -$\frac{1}{2}$＜-2＜0.02＜0 | B． | -$\frac{1}{2}$＜-2＜0＜0.02 | C． | -2＜-$\frac{1}{2}$＜0.02＜0 | D． | -2＜-$\frac{1}{2}$＜0＜0.02 |
19．若袋中装有2个红球和2个白球，搅匀后从袋中摸出一个球后，放回，然后再摸出一个球，则两次摸出的球都是红球的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
6．
如图，在△ABC中，点D，E分别在AB，AC上，则添加下面的条件后，不能判断△AED∽△ABC的是（ ）
如图，在△ABC中，点D，E分别在AB，AC上，则添加下面的条件后，不能判断△AED∽△ABC的是（ ）| A． | $\frac{AD}{AC}$=$\frac{DE}{BC}$ | B． | $\frac{AD}{AC}$=$\frac{AE}{AB}$ | C． | ∠AED=∠B | D． | ∠ADE=∠C |
3．已知三角形的两边长分别为3cm和8cm，则此三角形的第三边长可能是（ ）
| A． | 4cm | B． | 5cm | C． | 6cm | D． | 15cm |
4．一元二次方程x2+3x-2=0的根的情况是（ ）
| A． | 有两个不相等的实数根 | B． | 有两个相等的实数根 | ||
| C． | 没有实数根 | D． | 只有一个实数根 |