题目内容
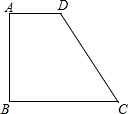 如图,直角梯形ABCD中,∠B=90°,AD∥BC,并且AD+BC=CD,求证:以AB为直径的⊙O与斜腰CD相切.
如图,直角梯形ABCD中,∠B=90°,AD∥BC,并且AD+BC=CD,求证:以AB为直径的⊙O与斜腰CD相切.考点:切线的判定
专题:证明题
分析:如图,作辅助线;运用面积公式列出等量关系,得到点O到DC的距离等于以AB为直径的⊙O的半径,问题即可解决.
解答: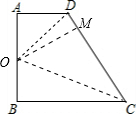 证明:如图,取AB的中点O,
证明:如图,取AB的中点O,
过点O作OM⊥CD,连接OD、OC;
设梯形ABCD、△OAD、△OBC、
△OCD的面积分别为α、β、γ、θ;
则α=
(AD+BC)AB=
(AD+BC)×2OA,
∵AB=2OA(设OA为λ),AD+BC=CD,
∴α=λCD;
又∵β=
AD•λ,γ=
BC•λ,θ=
CD•OM,
且α=β+γ+θ,
∴λCD=
(AD+BC)λ+
CD•OM,
而AD+BC=CD,
∴2λ=λ+OM,
∴OM=λ,即点O到DC的距离等于以AB为直径的⊙O的半径,
∴以AB为直径的⊙O与斜腰CD相切.
 证明:如图,取AB的中点O,
证明:如图,取AB的中点O,过点O作OM⊥CD,连接OD、OC;
设梯形ABCD、△OAD、△OBC、
△OCD的面积分别为α、β、γ、θ;
则α=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=2OA(设OA为λ),AD+BC=CD,
∴α=λCD;
又∵β=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
且α=β+γ+θ,
∴λCD=
| 1 |
| 2 |
| 1 |
| 2 |
而AD+BC=CD,
∴2λ=λ+OM,
∴OM=λ,即点O到DC的距离等于以AB为直径的⊙O的半径,
∴以AB为直径的⊙O与斜腰CD相切.
点评:该题主要考查了切线的判定及其应用问题;解题的关键是作辅助线,灵活选用切线的判定方法;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
已知点A的坐标为(1,2),点B的坐标为(2,2),反比列函数y=
的图象与线段AB相交.则k的取值范围为( )
| k |
| x |
| A、k<2 | B、k≤4 |
| C、k<2或k>4 | D、2≤k≤4 |
下列电视台台标的图案中,是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,直线AB、MN、PQ相交于点O,∠BOM是它的余角的2倍,∠AOP=2∠MOQ,且有OG⊥OA,求∠POG的度数.
如图,直线AB、MN、PQ相交于点O,∠BOM是它的余角的2倍,∠AOP=2∠MOQ,且有OG⊥OA,求∠POG的度数.