题目内容
2.已知平行四边形ABCD的对角线AC,BD相交于点O,AB=4,AO=3,BO=5,则平行四边形面积是24.分析 由平行四边形ABCD的对角线AC,BD相交于点O,AB=4,AO=3,BO=5,可证得AB⊥AC,继而求得答案.
解答 解:∵平行四边形ABCD的对角线AC,BD相交于点O,
∴AB=CD=4,AD=BC,AC=2AO=6,BD=2BO=10,
∵AB=4,AO=3,BO=5,
∴BO2=AB2+AO2,
∴∠OAB=90°,
即AB⊥AC,
∴平行四边形的面积=AB•AC=4×6=24.
故答案为:24.
点评 此题考查了平行四边形的性质、勾股定理的逆定理、直角三角形的判定.此题难度适中,注意掌握定理的应用是关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
12.已知$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$是方程组$\left\{\begin{array}{l}{2x+(m-1)y=2}\\{nx+y=1}\end{array}\right.$的解,则(m+n)2017的值为( )
| A. | 22017 | B. | -1 | C. | 1 | D. | 0 |
17.下来根式中,为最简二次根式的是( )
| A. | $\sqrt{11}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{20}$ |
14.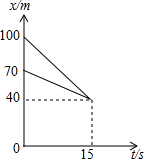 在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊,如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s),根据相关信息判断,下列说法中错误的是( )
在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊,如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s),根据相关信息判断,下列说法中错误的是( )
 在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊,如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s),根据相关信息判断,下列说法中错误的是( )
在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊,如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s),根据相关信息判断,下列说法中错误的是( )| A. | 灰太狼追上喜羊羊时,喜羊羊跑了60m | |
| B. | 喜羊羊与灰太狼最初的距离是30m | |
| C. | 灰太狼跑了60m追上了喜羊羊 | |
| D. | 灰太狼用15s追上了喜羊羊 |
11.下列各组长度的线段中,不能够组成直角三角形的一组是( )
| A. | 9,12,15 | B. | 7,24,25 | C. | $\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$ | D. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ |